Question

20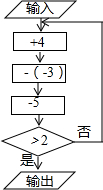．如图是一个数值转换机，输入数值后按三个方框中的程序运算，若第一次运算结果大于2，可以输出结果，则称该数只要“算一遍”；若第一次运算无法输出结果，且第二次运算结果大于2，可以输出结果，则称该数需要“算两遍”，以此类推：
（1）当输入数为2时，输出的结果为4；
（2）当输入数为-1时，求输出的结果；
（3）当输入数为x时，该数需要算两遍，直接写出x的取值范围．

Answer 1

分析 （1）根据程序运算得到算式2+4-（-3）-5计算即可；
（2）根据程序运算得到算式-1+4-（-3）-5=1，再根据程序运算得到算式1+4-（-3）-5计算即可；
（3）根据程序运算得到算式x+4-（-3）-5=x+2≤2，再根据程序运算得到算式x+2+4-（-3）-5=x+4＞2，解不等式即可得到x的取值范围．

解答 解：（1）依题意有
2+4-（-3）-5=4．
故答案为：4；
（2）依题意有
-1+4-（-3）-5=1，
1+4-（-3）-5=3．
故输出的结果是3；
（3）依题意有
x+4-（-3）-5=x+2≤2，
解得x≤0，
x+2+4-（-3）-5=x+4＞2，
解得x＞-2．
故x的取值范围是-2＜x≤0．

点评 本题考查了有理数的混合运算，解题关键是弄清题意，根据题意把输入数代入，按程序一步一步计算．