题目内容
10.已知:二次函数y=x2+bx+c的图象经过点A(2,5),B(0,3)(1)求此二次函数的解析式;
(2)求出该抛物线与x轴的交点坐标;
(3)直接写出当-3≤x≤1时,y的取值范围.
分析 (1)将点A(2,5),B(0,3)代入y=x2+bx+c,用待定系数法即可求得二次函数的解析式;
(2)令y=0,则0=x2-x+3,根据b2-4ac=1-3×4=-11<0,进而得出此二次函数与x轴无交点;
(3)由(2)可知y>0,即可求得当-3≤x≤1时,y>0.
解答 解:(1)把点A(2,5),B(0,3)代入y=x2+bx+c,
得$\left\{\begin{array}{l}{4+2b+c=5}\\{c=3}\end{array}\right.$,
解得b=-1,c=3,
∴二次函数解析式为y=x2-x+3.
(2)令y=0,则0=x2-x+3,
∵b2-4ac=1-3×4=-11<0,
∴该抛物线与x轴无交点;
(3)∵抛物线开口向上,与x轴无交点,
∴当-3≤x≤1时,y>0.
点评 本题考查了用待定系数法求二次函数的解析式,抛物线与x轴的交点坐标,熟练掌握待定系数法是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
20.下列各式中,运算结果等于x2-4x-12的是( )
| A. | (x+3)(x-4) | B. | (x-2)(x+6) | C. | (x-3)(x+4) | D. | (x+2)(x-6) |
18.一块矩形菜地的面积是120m2,如果它的长减少2m,那么菜地就变成正方形,则原菜地的长是( )
| A. | 10m | B. | 11m | C. | 12m | D. | 13m |
15.若|a+3|+(b-2)2=0,则ab的值为( )
| A. | -9 | B. | 9 | C. | -8 | D. | 8 |
19.下列选项中,是同类项的是( )
| A. | 3ab和3b | B. | -2pq和npq | C. | b2和2b | D. | 4xy和xy |
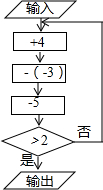 如图是一个数值转换机,输入数值后按三个方框中的程序运算,若第一次运算结果大于2,可以输出结果,则称该数只要“算一遍”;若第一次运算无法输出结果,且第二次运算结果大于2,可以输出结果,则称该数需要“算两遍”,以此类推:
如图是一个数值转换机,输入数值后按三个方框中的程序运算,若第一次运算结果大于2,可以输出结果,则称该数只要“算一遍”;若第一次运算无法输出结果,且第二次运算结果大于2,可以输出结果,则称该数需要“算两遍”,以此类推: