题目内容
7.先化简,再求值:(1-$\frac{1}{a+2}$)÷$\frac{{a}^{2}-1}{a+2}$,其中a=3.分析 先计算括号里面的,再把分子、分母因式分解,约分即可,把a=3代入计算即可.
解答 解:原式=$\frac{a+1}{a+2}$×$\frac{a+2}{(a+1)(a-1)}$
=$\frac{1}{a-1}$,
当a=3时,原式=$\frac{1}{3-1}$=$\frac{1}{2}$.
点评 本题考查了分式的化简求值,解答此题的关键是把分式化到最简,然后代值计算.

练习册系列答案
相关题目
15. 如图,是某几何体的俯视图,该几何体可能是( )
如图,是某几何体的俯视图,该几何体可能是( )
 如图,是某几何体的俯视图,该几何体可能是( )
如图,是某几何体的俯视图,该几何体可能是( )| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 正方体 |
12.某学校小组5名同学的身高(单位:cm)分别为:147,151,152,156,159,则这组数据的中位数是( )
| A. | 147 | B. | 151 | C. | 152 | D. | 156 |
19.在数轴上表示-2的点与表示3的点之间的距离是( )
| A. | 5 | B. | -5 | C. | 1 | D. | -1 |
16.在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.下图是由边长为1的正方形按照某种规律排列而成.

(1)观察图形,填写下表:
(2)推测第n个图形中,正方形的个数为5n+3,周长为10n+8;
(3)根据上述规律排列,是否存在一个图形,它的周长为2014?

(1)观察图形,填写下表:
| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
(3)根据上述规律排列,是否存在一个图形,它的周长为2014?
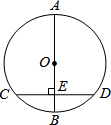 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=4-$\sqrt{7}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=4-$\sqrt{7}$.