题目内容
5.下图是由边长为1的正方形按照某种规律排列而成.
(1)观察图形,填写下表:
| 图形 | ① | ② | ③ |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
(3)根据上述规律排列,是否存在一个图形,它的周长为2014?
分析 (1)依次数出n=1,2,3,…,正方形的个数,算出图形的周长;
(2)根据(1)规律依此类推,可得出第n个图形中,正方形的个数及周长;
(3)周长为2014时,代入(2)得到的代数式列方程求解即可判断.
解答 解:(1)填表如下:
| 图形个数(n) | (1) | (2) | (3) |
| 正方形的个数 | 8 | 13 | 18 |
| 图形的周长 | 18 | 28 | 38 |
推测第n个图形中,正方形的个数为5n+3,周长为10n+8.
故答案为:5n+3,10n+8.
(3)周长为2014时,则2014=10n+8,解得n=$\frac{1003}{5}$,
因为n不是整数,所以不存在一个图形,它的周长为2014.
点评 本题考查图形的变化规律,解题思维过程是从特殊情况入手→探索、发现规律→归纳、猜想出结果→取特殊值代入验证,即体现特殊→一般→特殊的解题过程.

练习册系列答案
 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
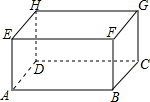 现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.则蜘蛛从表面迅速地捕到小虫的最短路程是$\sqrt{74}$.
现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).现在箱外的点A处有一只蜘蛛,箱内的点G处有一只小虫正在午睡,保持不动.则蜘蛛从表面迅速地捕到小虫的最短路程是$\sqrt{74}$. 如图,在平面直角坐标系中,△OAB顶点的坐标为O(0,0),A(3,2),B(0,2)(正方形网格的每个小正方形的边长都是1个单位长度)
如图,在平面直角坐标系中,△OAB顶点的坐标为O(0,0),A(3,2),B(0,2)(正方形网格的每个小正方形的边长都是1个单位长度) 如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若OB2-AB2=10,则k的值为5.
如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数y=$\frac{k}{x}$(k>0)的图象上,若OB2-AB2=10,则k的值为5.