题目内容
18.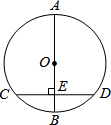 如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=4-$\sqrt{7}$.
如图,AB是⊙O的直径,弦CD⊥AB于点E,若AB=8,CD=6,则BE=4-$\sqrt{7}$.
分析 连接OC,根据垂径定理得出CE=ED=$\frac{1}{2}$CD=3,然后在Rt△OEC中由勾股定理求出OE的长度,最后由BE=OB-OE,即可求出BE的长度.
解答  解:如图,连接OC.
解:如图,连接OC.
∵弦CD⊥AB于点E,CD=6,
∴CE=ED=$\frac{1}{2}$CD=3.
∵在Rt△OEC中,∠OEC=90°,CE=3,OC=4,
∴OE=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$,
∴BE=OB-OE=4-$\sqrt{7}$.
故答案为4-$\sqrt{7}$.
点评 本题主要考查了垂径定理,勾股定理等知识,关键在于熟练的运用垂径定理得出CE、ED的长度.

练习册系列答案
相关题目
9.已知∠A=40°,则它的余角为( )
| A. | 40° | B. | 50° | C. | 130° | D. | 140° |
6.函数y=$\frac{{\sqrt{x}}}{2}$中,自变量x的取值范围是( )
| A. | x>0 | B. | x≥0 | C. | x<0 | D. | x≤0 |
13.在△ABC中,AB=12$\sqrt{2}$,AC=13,cos∠B=$\frac{{\sqrt{2}}}{2}$,则BC边长为( )
| A. | 7 | B. | 8 | C. | 8或17 | D. | 7或17 |
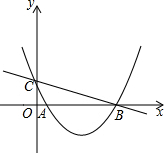 如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.
如图,已知抛物线y=ax2-5ax+2(a≠0)与y轴交于点C,与x轴交于点A(1,0)和点B.