题目内容
9. 如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB.
如图,AB=AC,∠BAC=120°,AD⊥AC,AE⊥AB.(1)求∠C的度数;
(2)求证:△ADE是等边三角形.
分析 (1)因为AB=AC,根据等腰三角形的性质,等腰三角形的两个底角相等,又∠BAC=120°,根据三角形内角和,可求出∠C的度数为30°.
(2)AD⊥AC,AE⊥AB,∠ADE=∠AED=60°,三个角是60°的三角形是等边三角形.
解答 (1)解:∵AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
故答案为:30°.
(2)证明:∵∠B=∠C=30°,AD⊥AC,AE⊥AB.
∴∠ADC=∠AEB=60°,
∴∠ADC=∠AEB=∠EAD=60°,
∴△ADE是等边三角形.
点评 本题考查等腰三角形的性质,等腰三角形的底角相等,以及等边三角形的判定定理,三个角是60°的三角形,是等边三角形.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
4.下列说法正确的是( )
| A. | 明天下雨的概率大 | |
| B. | 任意抛掷两颗完全相同的均匀的正四面体骰子,其点数之和为11的概率为零 | |
| C. | 随机说出3个正整数,以这三个数为边长一定能围成一个三角形 | |
| D. | 一副扑克牌,去掉大小王,从中任抽一张,恰好抽到的牌是10的概率为$\frac{1}{13}$ |
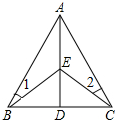 如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠1=∠2,试判断AD与BC的位置关系,并说明理由.
如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠1=∠2,试判断AD与BC的位置关系,并说明理由.