题目内容
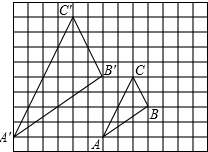如图，图中的小方格都是边长为1的正方形，△ABC与△A′B′C′的顶点都在格点上．（1）求证：△ABC∽A′B′C′；
（2）A′B′C′与△ABC是位似图形吗？如果是，在图形上画出位似中心并求出位似比．
考点：作图-位似变换
专题：
分析：（1）分别求出三角形各边长，进而得出答案；
（2）利用位似图形的性质得出答案．
（2）利用位似图形的性质得出答案．
解答：
（1）证明：∵AB=
，BC=
，AC=2
，A′B′=2
，B′C′=2
，A′C′=4
，
∴
=
=
=
，
∴△ABC∽A′B′C′；
（2）解：如图所示：两三角形对应点的连线相交于一点，故A′B′C′与△ABC是位似图形，O即为位似中心，
位似比为：2．
（1）证明：∵AB=| 13 |
| 5 |
| 5 |
| 13 |
| 5 |
| 5 |
∴
| AB |
| A′B′ |
| BC |
| B′C′ |
| AC |
| A′C′ |
| 1 |
| 2 |
∴△ABC∽A′B′C′；
（2）解：如图所示：两三角形对应点的连线相交于一点，故A′B′C′与△ABC是位似图形，O即为位似中心，
位似比为：2．
点评：此题主要考查了位似图形的性质以及相似三角形的判定，利用位似图形的定义得出是解题关键．
练习册系列答案
相关题目
将一根长为6cm的木棍分成两段，每段长分别为a，b（单位：cm）且a，b都为正整数．在直角坐标系中以a，b的值，构成点A（a，b）．那么点A落在抛物线y=-x2+6x-5与x轴所围成的封闭图形内部（如图，不含边界）的概率为
如图，?ABCD中，∠DAB的平分线交CD于点E，AE的中点是H，经过点E作AE的垂线交BC于G，交AB的延长线于点F，点G恰好是EF的中点，DH=GC．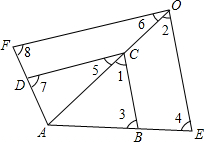
如图，已知△AEO∽△ABC，△AOF∽△ACD，那么四边形ABCD与四边形AEOF相似吗？请说明你的理由．
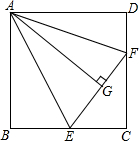如图正方形ABCD的边长为8cm，E是BC边的中点．把△ABE沿AE折叠到△AGE的位置，F是CD边上的一点，把△ADF沿AF折叠，D点恰好落在G点上，求CF的长度．
如图，△ABC内接于⊙O，且AC=AB，点D在