题目内容
 如图,?ABCD中,∠DAB的平分线交CD于点E,AE的中点是H,经过点E作AE的垂线交BC于G,交AB的延长线于点F,点G恰好是EF的中点,DH=GC.
如图,?ABCD中,∠DAB的平分线交CD于点E,AE的中点是H,经过点E作AE的垂线交BC于G,交AB的延长线于点F,点G恰好是EF的中点,DH=GC.(1)求证:∠HDC=∠ADH=∠C;
(2)若AE=6
| 3 |
考点:平行四边形的判定与性质,全等三角形的判定与性质
专题:
分析:(1)根据平行四边形的性质和平行线性质即可求解;
(2)可证CGE≌△BGF,即可求得EC的长,根据AE=ED即可求四边形ABCD的周长.
(2)可证CGE≌△BGF,即可求得EC的长,根据AE=ED即可求四边形ABCD的周长.
解答:解:(1)∵平行四边形ABCD,AE平分∠DAB;
∴∠DAE=∠EAF=∠AED;DC∥AB,
∴△DAE是等腰三角形,
∵E是AE的中点,
∴AD=DE;∠ADH=∠HDC;DH⊥AE,
又∵AE⊥EF,
∴DH∥EG,
∴四边形DEGH是平行四边形,
∴DH=EG;∠HDC=∠EGH,
∵EG=DH=CG,
∴△CGE是等腰三角形,
∴∠CEG=∠C=∠HDC=∠ADH;
(2)∵∠CEG=∠C=∠HDC=∠ADH且∠ADH+∠HDC+∠DAB=180°,
∴∠HDC=∠ADH=∠CEG=60°,
∴△CGE是等边三角形,
∵CE∥BF;G是EF中点,
在△CGE和△BGF中,
,
∴△CGE≌△BGF(AAS),
∴BG=CG=CE=DH.
∵AE=6
,
∴AH=3
;DE=AD=
AH=6,
∴BG=CG=CE=DH=
AD=3,
∴AD+DC=AD+DE+CE=6+6+3=15,
∴平行四边形ABCD的周长=2(AD+DC)=30.
∴∠DAE=∠EAF=∠AED;DC∥AB,
∴△DAE是等腰三角形,
∵E是AE的中点,
∴AD=DE;∠ADH=∠HDC;DH⊥AE,
又∵AE⊥EF,
∴DH∥EG,
∴四边形DEGH是平行四边形,
∴DH=EG;∠HDC=∠EGH,
∵EG=DH=CG,
∴△CGE是等腰三角形,
∴∠CEG=∠C=∠HDC=∠ADH;
(2)∵∠CEG=∠C=∠HDC=∠ADH且∠ADH+∠HDC+∠DAB=180°,
∴∠HDC=∠ADH=∠CEG=60°,
∴△CGE是等边三角形,
∵CE∥BF;G是EF中点,
在△CGE和△BGF中,
|
∴△CGE≌△BGF(AAS),
∴BG=CG=CE=DH.
∵AE=6
| 3 |
∴AH=3
| 3 |
| 2 | ||
|
∴BG=CG=CE=DH=
| 1 |
| 2 |
∴AD+DC=AD+DE+CE=6+6+3=15,
∴平行四边形ABCD的周长=2(AD+DC)=30.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角、对应边相等的性质.

练习册系列答案
相关题目
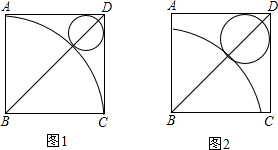
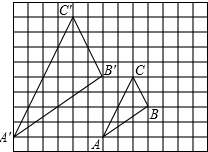 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.