题目内容
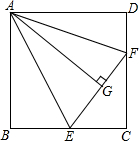 如图正方形ABCD的边长为8cm,E是BC边的中点.把△ABE沿AE折叠到△AGE的位置,F是CD边上的一点,把△ADF沿AF折叠,D点恰好落在G点上,求CF的长度.
如图正方形ABCD的边长为8cm,E是BC边的中点.把△ABE沿AE折叠到△AGE的位置,F是CD边上的一点,把△ADF沿AF折叠,D点恰好落在G点上,求CF的长度.考点:翻折变换(折叠问题)
专题:
分析:设CF=x,则DF=8-x,利用翻折变换的性质得出FG=DF=8-x,进而利用勾股定理得出FC的长.
解答:解:设CF=x,则DF=8-x,
∵△ABE折叠到△AGE,
∴△ABE≌△AGE,
∴BE=EG,
∵E是BC的中点,
∴BE=4,
∴EG=4,
∵△ADF沿AF折叠到G,
∴△ADF≌△AGF,
∴FG=DF=8-x,
在Rt△EFC中,
EF=4+8-x=12-x,
故42+x2=(12-x)2,
则16+x2=x2-24x+144,
解得:x=
,
即CF的长度为:
.
∵△ABE折叠到△AGE,
∴△ABE≌△AGE,
∴BE=EG,
∵E是BC的中点,
∴BE=4,
∴EG=4,
∵△ADF沿AF折叠到G,
∴△ADF≌△AGF,
∴FG=DF=8-x,
在Rt△EFC中,
EF=4+8-x=12-x,
故42+x2=(12-x)2,
则16+x2=x2-24x+144,
解得:x=
| 16 |
| 3 |
即CF的长度为:
| 16 |
| 3 |
点评:此题主要考查了翻折变换的性质以及勾股定理等知识,表示出EF的长是解题关键.

练习册系列答案
相关题目
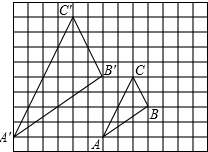 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上. 如图,在△ABC中,DE∥BC,AD=EC,BD=4,AE=3,求AB的长.
如图,在△ABC中,DE∥BC,AD=EC,BD=4,AE=3,求AB的长. 如图,在一个四边形各边上任意取一点,并顺次连接它们,想一想,你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?
如图,在一个四边形各边上任意取一点,并顺次连接它们,想一想,你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?