题目内容
 将一根长为6cm的木棍分成两段,每段长分别为a,b(单位:cm)且a,b都为正整数.在直角坐标系中以a,b的值,构成点A(a,b).那么点A落在抛物线y=-x2+6x-5与x轴所围成的封闭图形内部(如图,不含边界)的概率为
将一根长为6cm的木棍分成两段,每段长分别为a,b(单位:cm)且a,b都为正整数.在直角坐标系中以a,b的值,构成点A(a,b).那么点A落在抛物线y=-x2+6x-5与x轴所围成的封闭图形内部(如图,不含边界)的概率为考点:二次函数的性质,概率公式
专题:
分析:根据题意判定A的情况,然后求出在封闭图形内部的点A的个数,再根据概率公式计算即可得解.
解答:解:根据题意A的坐标共有5种情况:(1,5),(2,4),(3,3),(4,2),(5,1)
当x=1时,y=-x2+6x-5=0,(1,5)没在内部,
x=2时,y=-x2+6x-5=3,(2,4)没在内部,
x=3时,y=-x2+6x-5=4,(3,3)在内部,
x=4时,y=-x2+6x-5=3,(4,2)在内部,
x=5时,y=-x2+6x-5=0,(5,1)没有在内部,
所以,在封闭图形内部的点有1个,
P=
.
故答案为
.
当x=1时,y=-x2+6x-5=0,(1,5)没在内部,
x=2时,y=-x2+6x-5=3,(2,4)没在内部,
x=3时,y=-x2+6x-5=4,(3,3)在内部,
x=4时,y=-x2+6x-5=3,(4,2)在内部,
x=5时,y=-x2+6x-5=0,(5,1)没有在内部,
所以,在封闭图形内部的点有1个,
P=
| 2 |
| 5 |
故答案为
| 2 |
| 5 |
点评:本题考查了二次函数的性质,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目




 已知线段OA⊥OB,C为OB上中点,D为AO上一点,连AC、BD交于P点.当OA=OB,
已知线段OA⊥OB,C为OB上中点,D为AO上一点,连AC、BD交于P点.当OA=OB, 如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为
如图,⊙O的半径为4,A、B、C均是⊙O的点,点D是∠BAC的平分线与⊙O的交点,若∠BAC=120°,则弦BD的长为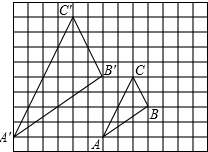 如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.
如图,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′的顶点都在格点上.