题目内容
12.已知二次函数y=ax2+bx+c(a≠0)中,函数值y与自变量x的部分对应值如下表:| x | … | -5 | -4 | -3 | -2 | -1 | … |
| y | … | 3 | -2 | -5 | -6 | -5 | … |
分析 根据图表求出函数对称轴,再根据图表信息和二次函数的对称性求出y值等于-2的自变量x的值即可.
解答 解:∵x=-3,x=-1的函数值都是-5,相等,
∴二次函数的对称轴为直线x=-2,
∵x=-4时,y=-2,
∴x=0时,y=-2,
∴方程ax2+bx+c=3的解是x1=-4,x2=0.
故答案为:x1=-4,x2=0.
点评 本题考查了二次函数的性质,主要利用了二次函数的对称性,读懂图表信息,求出对称轴解析式是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
20.在“2015高淳国际马拉松赛”中,有来自肯尼亚、韩国、德国等16个国家和地区约10100名马拉松爱好者参加,将10100用科学记数法可表示为( )
| A. | 10.1×103 | B. | 1.01×104 | C. | 1.01×105 | D. | 0.101×104 |



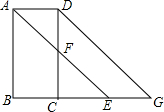 如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB
如图,已知∠BAD+∠ADC=180°,AE平分∠BAD,CD与AE相交于F,∠CFE=∠AEB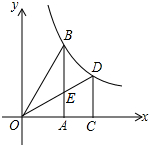 y=$\frac{3\sqrt{2}}{x}$.
y=$\frac{3\sqrt{2}}{x}$.