题目内容
3．一个几何体的三视图如图所示，该几何体的侧面积为（ ）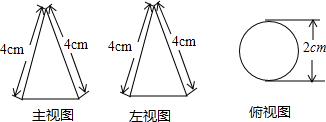
| A． | 2πcm2 | B． | 4πcm2 | C． | 8πcm2 | D． | 16πcm2 |
分析 由几何体的主视图和左视图都是等腰三角形，俯视图是圆，可以判断这个几何体是圆锥，进而得出圆锥的高以及母线长和底面圆的半径，再利用圆锥侧面积公式求出即可．
解答 解：依题意知母线l=4cm，底面半径r=2÷2=1，
则由圆锥的侧面积公式得S=πrl=π×1×4=4πcm2．
故选B．
点评 此题主要考查了三视图的知识和圆锥侧面面积的计算；解决此类图的关键是由三视图得到立体图形；学生由于空间想象能力不够，找不到圆锥的底面半径，或者对圆锥的侧面面积公式运用不熟练，易造成错误．
练习册系列答案
相关题目
11．
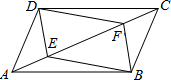如图，点E，F是□ABCD对角线上两点，在条件①DE=BF；②∠ADE=∠CBF；③AF=CE； ④∠AEB=∠CFD中，添加一个条件，使四边形DEBF是平行四边形，可添加的条件是（ ）
如图，点E，F是□ABCD对角线上两点，在条件①DE=BF；②∠ADE=∠CBF；③AF=CE； ④∠AEB=∠CFD中，添加一个条件，使四边形DEBF是平行四边形，可添加的条件是（ ）| A． | ①②③ | B． | ①②④ | C． | ①③④ | D． | ②③④ |
8．正六边形的外接圆半径为1，则它的内切圆半径为（ ）
| A． | $\sqrt{3}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{1}{2}$ | D． | 1 |
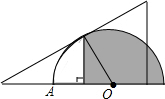如图，将一块含30°角的直角三角版和半圆量角器按如图的方式摆放，使斜边与半圆相切．若半径OA=4，则图中阴影部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$．（结果保留π）
13．下列计算，正确的是（ ）
| A． | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B． | |$\frac{1}{2}$-2|=-$\frac{3}{2}$ | C． | $\root{3}{8}$=2$\sqrt{2}$ | D． | （$\frac{1}{2}$）-1=2 |