题目内容
8. 在⊙O中,AB是直径,AC是切线且AC=AB,联结BC交⊙O于点D,试仅用无刻度直尺,作以D为切点的⊙O的切线DT.
在⊙O中,AB是直径,AC是切线且AC=AB,联结BC交⊙O于点D,试仅用无刻度直尺,作以D为切点的⊙O的切线DT.
分析 先连接AD,CO,交于点F,则点F为△ABC的重心,连接BF并延长,交AC于E,则E是AC的中点,BE是△ABC的中线,过点D,E作直线DT,连接OD,则直线DT即为所求.
解答 解:如图所示,连接CO、AD交于点F,连接BF并延长交AC于点E,过点D,E作直线DT,连接OD,则直线DT即为所求.
∵AB是⊙O的直径,AC是⊙O的切线,
∴AC⊥AB,
又∵AC=AB,
∴△ABC是等腰直角三角形,
连接AD,CO,交于点F,则AD⊥BC,
∴点D是BC的中点,
又∵O是AB的中点,
∴点F是△ABC的重心,
连接BF并延长,交AC于E,则E是AC的中点,
∴BE是△ABC的中线,
由题意知,△ABD、△ACD都是等腰直角三角形,
∴OD⊥AB,DE⊥AC,
又∵AB⊥AC,
∴∠ODE=90°,
∴DE是⊙O的切线.
点评 本题主要考查了切线的性质以及三角形重心的运用,解决问题的关键是掌握:圆的切线垂直于经过切点的半径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.“抛一枚质地均匀的硬币,落地后正面朝上”这一事件是( )
| A. | 确定事件 | B. | 必然事件 | C. | 不可能事件 | D. | 不确定事件 |
19.下列图形中,不是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
16.有一组数据:3,5,5,6,7,对这组数据分析错误的是( )
| A. | 众数是5 | B. | 中位数是5 | C. | 平均数是5 | D. | 极差是4 |
20.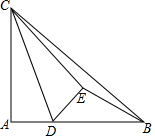 如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )
如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )
 如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )
如图,在Rt△ABC中,∠A=90°,AB=4,AC=3,D为AB上一动点,将△ACD沿CD翻折得到△ECD,那么BE的最小值为( )| A. | $\sqrt{3}$ | B. | 4-$\sqrt{3}$ | C. | $\sqrt{5}$ | D. | 2 |
 如图,在△ABC中,点D,E分别是边AB,AC上的点,且DE∥BC,若$\frac{AD}{DB}=\frac{1}{2}$,DE=3,则BC的长度是( )
如图,在△ABC中,点D,E分别是边AB,AC上的点,且DE∥BC,若$\frac{AD}{DB}=\frac{1}{2}$,DE=3,则BC的长度是( )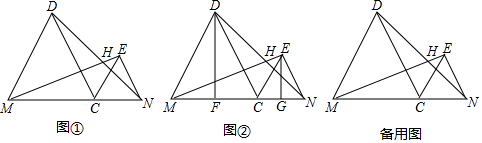
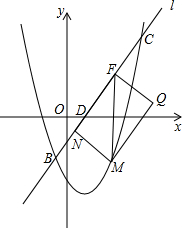 已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).
已知抛物线y=ax2+bx+c(a≠0)经过原点,顶点为A(h,k)(h≠0).