题目内容
6.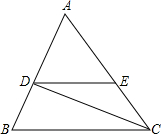 已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.
已知:如图,CD是∠ACB的平分线,∠ACB=48°,∠BDC=82°,DE∥BC.求:(1)∠EDC的度数;
(2)∠B的度数.
分析 (1)由CD是∠ACB的平分线,∠ACB=48°,根据角平分线的性质,即可求得∠DCB的度数,又由DE∥BC,根据两直线平行,内错角相等,即可求得∠EDC的度数;
(2)根据三角形的内角和即可求得∠B的度数.
解答 解:(1)∵CD是∠ACB的平分线,∠ACB=48°,
∴∠BCD=$\frac{1}{2}$∠ACB=24°,
∵DE∥BC,
∴∠EDC=∠DCB=24°,
∵∠BDC=82°,
∴∠EDC=24°,
(2)∴∠B=180°-∠EDC-∠BDC=180°-24°-82°=74°.
点评 此题考查了平行线的性质与角平分线的定义.解此题的关键是掌握两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
17.一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球是白球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
15.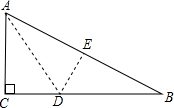 如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
 如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )
如图,一中江县进行纸片,AC=6cm,AB=10cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于( )| A. | 3cm | B. | 5cm | C. | 3$\sqrt{5}$cm | D. | 9$\sqrt{5}$cm |

 某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米?
某宾馆铺地毯,已知主楼梯宽3米,其余数据如图所示,需购地毯多少平方米? 如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上.
如图,我南海某海域A处有一艘捕鱼船在作业时突遇特大风浪,船长马上向我国渔政搜救中心发出求救信号,此时一艘渔政船正巡航到捕鱼船正西方向的B处,该渔政船收到渔政求救中心指令后前去救援,但两船之间有大片暗礁,无法直线到达,于是决定马上调整方向,先向北偏东60°方向以每小时30海里的速度航行半小时到达C处,同时捕鱼船低速航行到A点的正北1.5海里D处,渔政船航行到点C处时测得点D在南偏东53°方向上. 如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD=6.
如图,在平行四边形ABCD中,AC⊥BC,E为AB的中点,若CE=5,AC=8,则AD=6.