题目内容
18.将抛物线y=x2向下平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式是( )| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
分析 根据函数图象向下平移减,向右平移减,可得答案.
解答 解:将抛物线y=x2向下平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式是y=(x-2)2-3,
故选:A.
点评 本题考查了二次函数图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
9.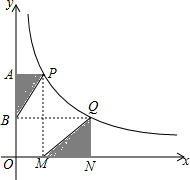 如图,点P、Q是反比例函数y=$\frac{k}{x}$(k≠0)图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记S△ABP=S1,S△QMN=S2,则S1与S2的大小关系为( )
如图,点P、Q是反比例函数y=$\frac{k}{x}$(k≠0)图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记S△ABP=S1,S△QMN=S2,则S1与S2的大小关系为( )
 如图,点P、Q是反比例函数y=$\frac{k}{x}$(k≠0)图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记S△ABP=S1,S△QMN=S2,则S1与S2的大小关系为( )
如图,点P、Q是反比例函数y=$\frac{k}{x}$(k≠0)图象上的两点,PA⊥y轴于点A,QN⊥x轴于点N,作PM⊥x轴于点M,QB⊥y轴于点B,连接PB、QM,记S△ABP=S1,S△QMN=S2,则S1与S2的大小关系为( )| A. | S1>S2 | B. | S1<S2 | C. | S1=S2 | D. | 无法判定 |
10.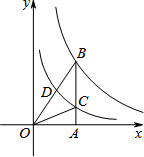 如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
 如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )
如图所示,在平面坐标系中,AB⊥x轴,反比例函数y=$\frac{{k}_{1}}{x}$(k1≠0)过B点,反比例函数y=$\frac{{k}_{2}}{x}$(k2≠0)过C、D点,OC=BC,B(2,3),则D点的坐标为( )| A. | ($\frac{3}{2}$,$\frac{5}{9}$) | B. | ($\frac{\sqrt{5}}{3}$,$\frac{\sqrt{5}}{2}$) | C. | ($\frac{4}{3}$,$\frac{5}{4}$) | D. | ($\frac{\sqrt{10}}{3}$,$\frac{\sqrt{10}}{2}$) |
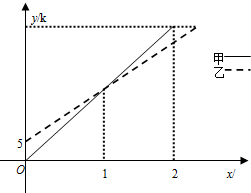 在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.两人在出发时都配备了通话距离为3km的对讲机,便于两人在骑车过程中可以用对讲机通话.下列说法:
在一条直线上依次有A、B、C三地,自行车爱好者甲、乙两人同时分别从A、B两地出发,沿直线匀速骑向C地.已知甲的速度为20km/h,设甲、乙两人行驶x(h)后,与A地的距离分别为y1、y2(km),y1、y2与x的函数关系如图所示.两人在出发时都配备了通话距离为3km的对讲机,便于两人在骑车过程中可以用对讲机通话.下列说法:
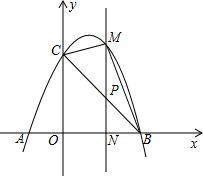 如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
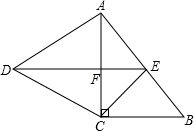 如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE,与AC相交于点F.
如图,在Rt△ABC中,∠ACB=90°,以AC为一边向外作等边三角形ACD,点E为AB的中点,连结DE,与AC相交于点F.