题目内容
6.吸烟有害健康,为配合“戒烟”运动,某校组织同学们在社区开展了“你支持哪种戒烟方式”的随机问卷调查,并将调查结果绘制成两幅不完整的统计图: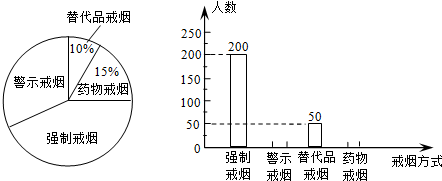
根据统计图解答下列问题:
(1)同学们一共调查了多少人?
(2)将条形统计图补充完整.
(3)若该社区有1万人,请你估计大约有多少人支持“警示戒烟”这种方式?
分析 (1)根据支持替代品戒烟的人数是50,所占的百分比是10%,即可求得总人数;
(2)利用百分比的意义求得支持药物戒烟的人数,利用总人数减去其它组的人数即可求得支持警示戒烟的人数;
(3)利用总人数乘以对应的百分比即可.
解答 解:(1)调查的总人数是:50÷10%=500(人);
(2)药物戒烟的人数是:500×15%=75(人);
支持警示戒烟的人数是:500-200-50-75=175(人). ;
;
(3)估计支持“警示戒烟”这种方式的人数是:10000×$\frac{175}{500}$=3500(人).
答:估计支持“警示戒烟”这种方式的人数是3500人.
点评 本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.

练习册系列答案
相关题目
1.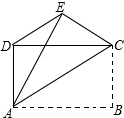 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
11.用换元法解方程$\frac{y}{{y}^{2}-3}$+$\frac{{y}^{2}-3}{y}$=$\frac{5}{2}$时,如果设x=$\frac{y}{{y}^{2}-3}$,那么原方程可化为( )
| A. | 2x2-5x+2=0 | B. | x2-5x+1=0 | C. | 2x2+5x+2=0 | D. | 2x2-5x+1=0 |
18.将抛物线y=x2向下平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式是( )
| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
15.对甲、乙两户家庭全年各项支出的统计如图所示,已知甲户居民的衣着支出与乙户相同,下面根据统计,对两户家庭教育支出的费用做出判断,正确的是( )
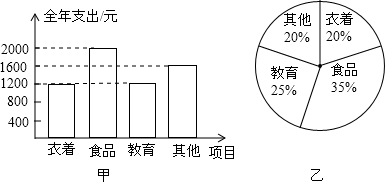

| A. | 甲比乙大 | B. | 乙比甲大 | C. | 甲、乙一样大 | D. | 无法确定 |
16.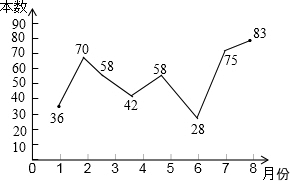 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )| A. | 阅读数量的平均数是57 | B. | 阅读数量的众数是42 | ||
| C. | 阅读数量的中位数是58 | D. | 有4个月的阅读数量超过60本 |
 配方后所得的方程是
配方后所得的方程是 B.
B.  C.
C.  D.
D. 