题目内容
13.已知线段AB=10,P是线段AB的黄金分割点(AP>PB),则AP=5$\sqrt{5}$-5.分析 直接根据黄金分割的定义计算.
解答 解:∵P是线段AB的黄金分割点(AP>PB),
∴AP=$\frac{\sqrt{5}-1}{2}$AB=$\frac{\sqrt{5}-1}{2}$×10=5$\sqrt{5}$-5.
故答案为5$\sqrt{5}$-5.
点评 本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=$\frac{\sqrt{5}-1}{2}$AB≈0.618AB,并且线段AB的黄金分割点有两个.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
4.若a1=1-$\frac{1}{m}$,a2=1-$\frac{1}{{a}_{1}}$,a3=1-$\frac{1}{{a}_{2}}$,则a2015的值为( )
| A. | 1-$\frac{1}{m}$ | B. | -$\frac{1}{m-1}$ | C. | m | D. | $\frac{1}{m}$ |
1.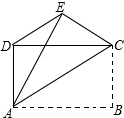 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
 如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )
如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE,若DE:AC=3:5,则AD:AB的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{8}$ | D. | $\frac{3}{4}$ |
18.将抛物线y=x2向下平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式是( )
| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
5.在二次函数y=ax2+bx+c,x与y的部分对应值如下表:
则下列说法:①图象经过原点;②图象开口向下;③图象经过点(-1,3);④当x>0时,y随x的增大而增大;⑤方程ax2+bx+c=0有两个不相等的实数根.其中正确的是( )
| x | … | -2 | 0 | 2 | 3 | … |
| y | … | 8 | 0 | 0 | 3 | … |
| A. | ①②③ | B. | ①③⑤ | C. | ①③④ | D. | ①④⑤ |

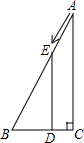 如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为4或7秒.
如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为4或7秒.
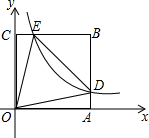 如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与正方形OABC的边AB、BC分别交于点D、E.若正方形OABC的边长为1,△ODE是等边三角形,则k的值为2-$\sqrt{3}$.
如图,已知反比例函数y=$\frac{k}{x}$(k>0)的图象与正方形OABC的边AB、BC分别交于点D、E.若正方形OABC的边长为1,△ODE是等边三角形,则k的值为2-$\sqrt{3}$.