题目内容
7.图①是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.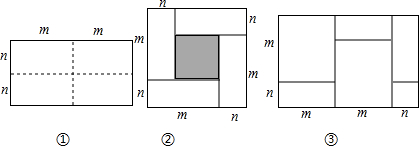
(1)图②中的阴影部分的面积为(m-n)2;
(2)观察图②,三个代数式(m+n)2,(m-n)2,mn之间的等量关系是(m+n)2-(m-n)2=4mn;
(3)观察图③,你能得到怎样的代数等式呢?
(4)试画出一个几何图形,使它的面积能表示(m+n)(m+3n);
(5)若x+y=-6,xy=2.75,求x-y的值.
分析 (1)可直接用正方形的面积公式得到.
(2)掌握完全平方公式,并掌握和与差的区别.
(3)可利用各部分面积和=长方形面积列出恒等式.
(4)此题可参照第(3)题.
(5)掌握完全平方公式,并掌握和与差的区别.
解答 解:(1)阴影部分的边长为(m-n),所以阴影部分的面积为(m-n)2;
故答案为:(m-n)2;
(2)(m+n)2-(m-n)2=4mn;
故答案为:(m+n)2-(m-n)2=4mn;
(3)(m+n)(2m+n)=2m2+3mn+n2;
(4)答案不唯一:
(5)(x-y)2=(x+y)2-4xy=(-6)2-2.75×4=25,
∴x-y=±5.
点评 本题考查了因式分解的应用,解题关键是认真观察题中给出的图示,用不同的形式去表示面积,熟练掌握完全平方公式,并能进行变形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.将抛物线y=x2向下平移3个单位,再向右平移2个单位,那么得到的抛物线的解析式是( )
| A. | y=(x-2)2-3 | B. | y=(x-2)2+3 | C. | y=(x+2)2-3 | D. | y=(x+2)2+3 |
15.对甲、乙两户家庭全年各项支出的统计如图所示,已知甲户居民的衣着支出与乙户相同,下面根据统计,对两户家庭教育支出的费用做出判断,正确的是( )
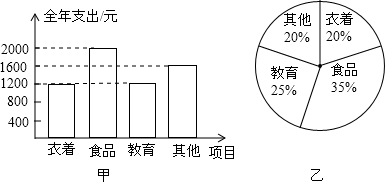

| A. | 甲比乙大 | B. | 乙比甲大 | C. | 甲、乙一样大 | D. | 无法确定 |
16.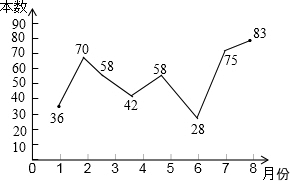 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )| A. | 阅读数量的平均数是57 | B. | 阅读数量的众数是42 | ||
| C. | 阅读数量的中位数是58 | D. | 有4个月的阅读数量超过60本 |
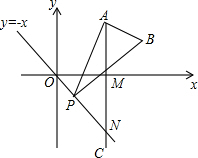 如图,已知点A的坐标为(3,3$\sqrt{3}$),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,若点P从点O出发,在线段ON上向点N运动时,B点也随之运动.
如图,已知点A的坐标为(3,3$\sqrt{3}$),AC⊥x轴于点M,交直线y=-x于点N,若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,若点P从点O出发,在线段ON上向点N运动时,B点也随之运动.