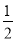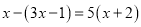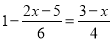题目内容
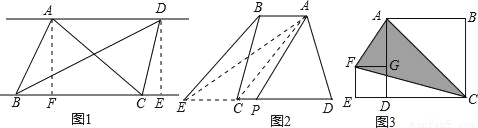
(1)自主阅读:在三角形的学习过程,我们知道三角形一边上的中线将三角形分成了两个面积相等三角形,原因是两个三角形的底边和底边上的高都相等,在此基础上我们可以继续研究:如图1,AD∥BC,连接AB,AC,BD,CD,则S△ABC=S△BCD.
证明:分别过点A和D,作AF⊥BC于F.DE⊥BC于E,由AD∥BC,可得AF=DE,又因为S△ABC=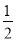 ×BC×AF,S△BCD=
×BC×AF,S△BCD= ×BC×DE .
×BC×DE .
所以S△ABC=S△BCD
由此我们可以得到以下的结论:像图1这样.
(2)问题解决:如图2,四边形ABCD中,AB∥DC,连接AC,过点B作BE∥AC,交DC延长线于点E,连接点A和DE的中点P,请你运用上面的结论证明:S?ABCD=S△APD
(3)应用拓展:
如图3,按此方式将大小不同的两个正方形放在一起,连接AF,CF,若大正方形的面积是80cm2,则图中阴影三角形的面积是 cm2.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目


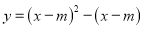 ,其中
,其中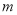 是常数,该抛物线的对称轴为直线
是常数,该抛物线的对称轴为直线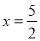 .
.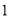 )求该抛物线的函数解析式.
)求该抛物线的函数解析式.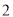 )把该抛物线沿
)把该抛物线沿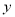 轴向上平移多少个单位后,得到的抛物线与
轴向上平移多少个单位后,得到的抛物线与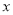 轴只有一个公共点.
轴只有一个公共点.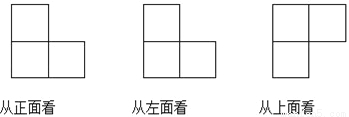
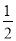 x+2与y轴交于点A,与直线y=﹣
x+2与y轴交于点A,与直线y=﹣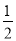 x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣
x交于点B,以AB为边向右作菱形ABCD,点C恰与原点O重合,抛物线y=(x﹣h)2+k的顶点在直线y=﹣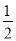 x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )
x上移动.若抛物线与菱形的边AB、BC都有公共点,则h的取值范围是( )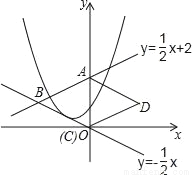
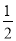 B. ﹣2≤h≤1 C. ﹣1≤h≤
B. ﹣2≤h≤1 C. ﹣1≤h≤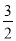 D. ﹣1≤h≤
D. ﹣1≤h≤