��Ŀ����
��֪������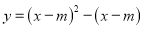 ������
������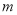 �dz������������ߵĶԳ���Ϊֱ��
�dz������������ߵĶԳ���Ϊֱ��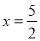 ��
��
��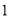 ����������ߵĺ�������ʽ��
����������ߵĺ�������ʽ��
��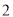 ���Ѹ���������
���Ѹ���������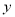 ������ƽ�ƶ��ٸ���λ�õ�����������
������ƽ�ƶ��ٸ���λ�õ�����������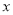 ��ֻ��һ�������㣮
��ֻ��һ�������㣮
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��֪������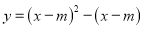 ������
������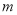 �dz������������ߵĶԳ���Ϊֱ��
�dz������������ߵĶԳ���Ϊֱ��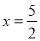 ��
��
��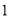 ����������ߵĺ�������ʽ��
����������ߵĺ�������ʽ��
��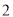 ���Ѹ���������
���Ѹ���������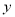 ������ƽ�ƶ��ٸ���λ�õ�����������
������ƽ�ƶ��ٸ���λ�õ�����������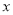 ��ֻ��һ�������㣮
��ֻ��һ�������㣮