Question

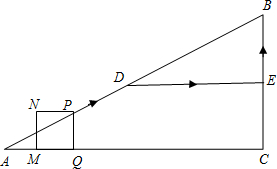
如图，在△ABC中，DE∥BC，CF∥AB．
（1）求证：△ABC∽△CFE；
（2）若D为AB的中点，求

S△ABC

S△CFE

的值．

Answer 1

考点：相似三角形的判定与性质

专题：

分析：（1）证明∠A=∠ECF，四边形BCFD为平行四边形，进而得到∠B=∠F，即可解决问题．
（2）证明AB=2CF，借助相似三角形的性质，即可解决问题．

解答：（1）证明：∵DE∥BC，CF∥AB，
∴∠A=∠ECF，四边形BCFD为平行四边形，
∴∠B=∠F，
∴△ABC∽△CFE．
（2）解：∵D为AB的中点，
∴AB=2BD；
∵四边形BCFD为平行四边形，
∴CF=BD，
∴AB=2CF；
∵△ABC∽△CFE，
∴

S△ABC

S△CFE

=(

AB

CF

)2=4，
即

S△ABC

S△CFE

的值=4．

点评：该题以平行四边形为载体，在考查平行四边形的性质及其应用的同时，还渗透了对相似三角形的判定及其性质的考查；对综合的分析问题解决问题的能力提出了较高的要求．