题目内容
 如图,已知第二象限内的点A在反比例函数y=
如图,已知第二象限内的点A在反比例函数y=| k |
| x |
| 2 |
| x |
(1)求△BOM的面积.
(2)若cos∠ABO=
| ||
| 5 |
考点:反比例函数综合题
专题:
分析:(1)根据S=
|k|即可求得;
(2)作AC⊥y轴,BD⊥y轴.易得△ACO∽△ODB,根据比例式求出BD,OD,可得出点B的坐标,代入y=
即可求出k的值.
| 1 |
| 2 |
(2)作AC⊥y轴,BD⊥y轴.易得△ACO∽△ODB,根据比例式求出BD,OD,可得出点B的坐标,代入y=
| k |
| x |
解答:解:(1)△BOM的面积=
×2=1;
(2)如图,作BD⊥y轴,AC⊥y轴.

∵OA⊥OB,
∴∠AOB=90°,
∵∠OAC+∠AOC=90°,∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△ACO∽△ODB,
∴
=
=
,
∵cos∠ABO=
,
∴
=
,
∴OB=
AB,
∴OA=
=
AB,
∴
=
=
=
,
设B(x,
)
AC=2OD=-
,OC=2BD=-2x,
∴A(
,-2x),
代入反比例函数y=
的图象上,得-2x=
,
解得k=-8.
| 1 |
| 2 |
(2)如图,作BD⊥y轴,AC⊥y轴.

∵OA⊥OB,
∴∠AOB=90°,
∵∠OAC+∠AOC=90°,∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
∴△ACO∽△ODB,
∴
| OA |
| OB |
| OC |
| BD |
| AC |
| OD |
∵cos∠ABO=
| ||
| 5 |
∴
| OB |
| AB |
| ||
| 5 |
∴OB=
| ||
| 5 |
∴OA=
| AB2-OB2 |
2
| ||
| 5 |
∴
| OA |
| OB |
| OC |
| BD |
| AC |
| OD |
| 2 |
| 1 |
设B(x,
| 2 |
| x |
AC=2OD=-
| 4 |
| x |
∴A(
| 4 |
| x |
代入反比例函数y=
| k |
| x |
| k | ||
|
解得k=-8.
点评:本题主要考查了相似三角形的判定与性质及反比例函数图象上点的坐标特征,解题的关键是正确作出辅助线,构造相似三角形.

练习册系列答案
相关题目
下列问题中,两个变量成正比例的是( )
| A、等腰三角形的面积一定,它的底边和底边上的高 |
| B、等边三角形的面积和它的边长 |
| C、长方形的一边长确定,它的周长与另一边长 |
| D、长方形的一边长确定,它的面积与另一边长 |
若函数y=
(k≠0)的图象过(
,3),则关于函数图象叙述正确的是( )
| k |
| x |
| 2 |
| A、当x≠0时,y随x的增大而增大 |
| B、分别在一、三象限内,y随x的增大而减小 |
| C、当x≠0时,y随x的增大而减小 |
| D、分别在二、四象限内,y随x的增大而增大 |
 如图,在△ABC中,DE∥BC,CF∥AB.
如图,在△ABC中,DE∥BC,CF∥AB.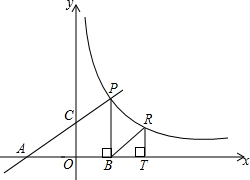 如图,直线y=
如图,直线y= 画出如图所示图形的三种视图(注:从正面、左面、上面看到的视图)
画出如图所示图形的三种视图(注:从正面、左面、上面看到的视图)