Question

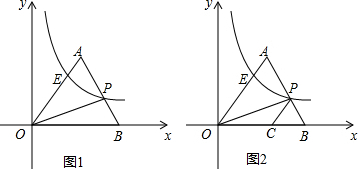
1．如图，在平面直角坐标系xOy中，△OAB如图放置，点P是AB边上的一点，过点P的反比例函数y=$\frac{k}{x}（k＞0，x＞0）$与OA边交于点E，连接OP．
（1）如图1，若点A的坐标为（3，4），点B的坐标为（5，0），且△OPB的面积为5，求直线AB和反比例函数y=$\frac{k}{x}$的解析式；
（2）如图2，若∠AOB=60°，过P作PC∥OA，与OB交于点C，若OE=4，并且△OPC的面积为$\frac{3\sqrt{3}}{2}$，求反比例函数y=$\frac{k}{x}$的解析式及点P的坐标．

Answer 1

分析 （1）过点P作PQ⊥x轴交x轴于点Q，利用待定系数法求出直线AB的解析式，根据△OPB的面积为5求出PQ的长，代入直线AB的解析式可得出P点坐标，进而可得出反比例函数的解析式；
（2）过点E作EF⊥x轴交x轴于点F，过点P作PS⊥x轴交x轴于点S，利用锐角三角函数的定义求出OF及EF的长，故可得出反比例函数的解析式，根据△OPC的面积为$\frac{3\sqrt{3}}{2}$求出OC•PS的长，再由锐角三角函数的定义得出PS的长，进而可得出P点坐标．

解答 解：（1）如图1，过点P作PQ⊥x轴交x轴于点Q，
∵点A的坐标为（3，4），点B的坐标为（5，0），
∴设直线AB的解析式为y=kx+b（k≠0），
∴$\left\{\begin{array}{l}3k+b=4\\ 5k+b=0\end{array}\right.$，解得$\left\{\begin{array}{l}k=-2\\ b=10\end{array}\right.$，
∴直线AB的解析式为：y=-2x+10．
∵点B的坐标为（5，0），且△OPB的面积为5，
∴PQ=2，点P纵坐标为2．                       
∵点P在直线AB上-2x+10=2，解得x=4，
∴点P坐标为（4，2）
∴此反比例函数的解析式为y=$\frac{8}{x}$；

（2）如图2，过点E作EF⊥x轴交x轴于点F，过点P作PS⊥x轴交x轴于点S，
∵∠AOB=60°，∠EFO=90°，OE=4，
∴OF=2，EF=2$\sqrt{3}$，
∴此反比例函数的解析式为y=$\frac{4\sqrt{3}}{x}$．
∵S_△OCP=$\frac{3\sqrt{3}}{2}$=$\frac{1}{2}$OC•PS，
∴OC•PS=3$\sqrt{3}$．
∵OS•PS=4$\sqrt{3}$，
∴CS•PS=$\sqrt{3}$．
∵∠AOB=60°  PC∥OA，
∴∠PCS=60°，
∴PS=$\sqrt{3}$CS，
∴CS=1．
∴点P坐标为（4，$\sqrt{3}$）．

点评 本题考查的是反比例函数与一次函数的交点问题，根据题意作出辅助线，构造出直角三角形，利用锐角三角函数的定义求解是解答此题的关键．