题目内容
6.在下面四个图形中,已知AB∥CD,(1)填空:各图中锐角∠P与∠A、∠C分别满足什么关系?①∠APC=360°-(∠A+∠C)②∠APC=∠A+∠C③∠P=∠C-∠A④∠P=∠A-∠C
(2)请你说明第四个关系如何是如何得到的?
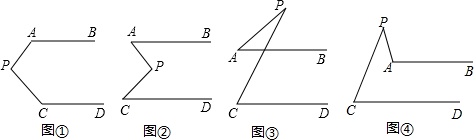
分析 (1)在图(1)(2)中可过P作平行线,根据平行线的性质可求得∠A与∠P、∠C的关系;在(3)中根据平行线的性质和三角形内角和定理可求得∠A与∠P、∠C的关系;在(4)中延长BA交PC于点E,利用平行线的性质和三角形外角的性质可求得∠A与∠P、∠C的关系;
(2)过点P作PE∥AB,得到PE∥CD,由平行线的性质得到∠C=∠EPC,∠EPA=∠A,而∠EPA=∠P+∠EPC,由此推出结论.
解答  解:(1)①过P作PE∥AB,
解:(1)①过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1+∠A=∠2+∠C=180°,
∴∠APC=360°-(∠A+∠C),
②过P作PE∥AB,
∵AB∥CD,
∴AB∥PE∥CD,
∴∠1=∠A,∠2=∠C,
∴∠APC=∠A+∠C,
③∵AB∥CD,
∴∠1=∠C,
∴∠P=∠1-∠A=∠C-∠A,
④延长BA交PC于E,
∵AB∥CD,
∴∠1=∠C,
∴∠PAB=∠P+∠1,
∴∠P=∠A-∠C;
故答案为:∠APC=360°-(∠A+∠C),∠APC=∠A+∠C,∠P=∠C-∠A,∠P=∠A-∠C;
(2)过点P作PE∥AB,
∵AB∥CD,
∴PE∥CD,
∴∠C=∠EPC,∠EPA=∠A,
而∠EPA=∠P+∠EPC,
∴∠A=∠P+∠C,
∠P=∠A-∠C.
点评 本题主要考查平行线的性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
16.如果点P(-5,y+1)在第三象限,则y的取值范围是( )
| A. | y<0 | B. | y>0 | C. | y>-1 | D. | y<-1 |
14.实数-2,0.101001,$\frac{1}{7}$,$\sqrt{2}$,-π中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |



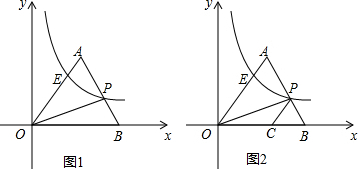
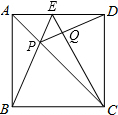 如图,已知正方形ABCD,E为AD的中点,连接BE和EC,BE交AC于点P,连接DP,交CE于Q.求证:
如图,已知正方形ABCD,E为AD的中点,连接BE和EC,BE交AC于点P,连接DP,交CE于Q.求证: 正方形ABCD中,点G为BC上任意一点,DE⊥AG于E,BF∥DE交AG于F.
正方形ABCD中,点G为BC上任意一点,DE⊥AG于E,BF∥DE交AG于F.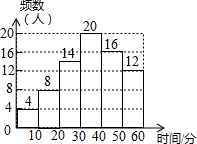 小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.
小文同学统计了他所在小区居民每天微信阅读的时间,并绘制了直方图.