题目内容
9. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )| A. | 大于0 | B. | 等于0 | C. | 小于0 | D. | 不能确定 |
分析 设ax2+bx+c=0(a≠0)的两根为x1,x2,由二次函数的图象可知x1+x2>0,a>0,设方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根为m,n再根据根与系数的关系即可得出结论.
解答 解:设ax2+bx+c=0(a≠0)的两根为x1,x2,
∵由二次函数的图象可知x1+x2>0,a>0,
∴-$\frac{b}{a}$>0.
设方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根为m,n,则m+n=-$\frac{b-\frac{2}{3}}{a}$=-$\frac{b}{a}$+$\frac{2}{3a}$,
∵a>0,
∴$\frac{2}{3a}$>0,
∴m+n>0.
故选A.
点评 本题考查的是抛物线与x轴的交点,熟知抛物线与x轴的交点与一元二次方程根的关系是解答此题的关键.

练习册系列答案
相关题目
20.下列运算中,计算正确的是( )
| A. | 2a•3a=6a | B. | (3a2)3=27a6 | C. | a4÷a2=2a | D. | (a+b)2=a2+ab+b2 |
4.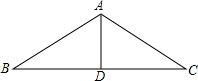 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
 如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )| A. | 5sin36°米 | B. | 5cos36°米 | C. | 5tan36°米 | D. | 10tan36°米 |
1.一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4随机摸出一个小球,不放回,再随机摸出一个小球,两次摸出的小球标号的积小于4的概率是( )
| A. | $\frac{1}{6}$ | B. | $\frac{5}{16}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.