题目内容
4．
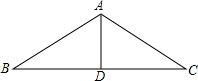如图，厂房屋顶人字形（等腰三角形）钢架的跨度BC=10米，∠B=36°，则中柱AD（D为底边中点）的长是（ ）| A． | 5sin36°米 | B． | 5cos36°米 | C． | 5tan36°米 | D． | 10tan36°米 |
分析 根据等腰三角形的性质得到DC=BD=5米，在Rt△ABD中，利用∠B的正切进行计算即可得到AD的长度．
解答 解：∵AB=AC，AD⊥BC，BC=10米，
∴DC=BD=5米，
在Rt△ADC中，∠B=36°，
∴tan36°=$\frac{AD}{BD}$，即AD=BD•tan36°=5tan36°（米）．
故选：C．
点评 本题考查了解直角三角形的应用．解决此问题的关键在于正确理解题意的基础上建立数学模型，把实际问题转化为数学问题．
练习册系列答案
相关题目
二次函数y=ax2+bx+c（a≠0）和正比例函数y=$\frac{2}{3}$x的图象如图所示，则方程ax2+（b-$\frac{2}{3}$）x+c=0（a≠0）的两根之和（ ）
如图，在平面直角坐标系xOy中，抛物线y=x2+$\frac{1}{4}$与y轴相交于点A，点B与点O关于点A对称