题目内容
17. 如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
如图,矩形ABCD中,BC=2,将矩形ABCD绕点D顺时针旋转90°,点A、C分别落在点A′、C′处.如果点A′、C′、B在同一条直线上,那么tan∠ABA′的值为$\frac{\sqrt{5}-1}{2}$.
分析 设AB=x,根据平行线的性质列出比例式求出x的值,根据正切的定义求出tan∠BA′C,根据∠ABA′=∠BA′C解答即可.
解答 解: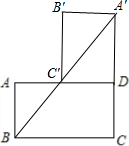 设AB=x,则CD=x,A′C=x+2,
设AB=x,则CD=x,A′C=x+2,
∵AD∥BC,
∴$\frac{C′D}{BC}$=$\frac{A′D}{A′C}$,即$\frac{x}{2}$=$\frac{2}{x+2}$,
解得,x1=$\sqrt{5}$-1,x2=-$\sqrt{5}$-1(舍去),
∵AB∥CD,
∴∠ABA′=∠BA′C,
tan∠BA′C=$\frac{BC}{A′C}$=$\frac{2}{\sqrt{5}-1+2}$=$\frac{\sqrt{5}-1}{2}$,
∴tan∠ABA′=$\frac{\sqrt{5}-1}{2}$,
故答案为:$\frac{\sqrt{5}-1}{2}$.
点评 本题考查的是旋转的性质、矩形的性质以及锐角三角函数的定义,掌握旋转前、后的图形全等以及锐角三角函数的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.如图,用黑白两种颜色的菱形纸片,按黑色纸片数逐渐增加1的规律拼成下列图案,若第n个图案中有2017个白色纸片,则n的值为( )


| A. | 671 | B. | 672 | C. | 673 | D. | 674 |
2.据《南国早报》报道:2016年广西高考报名人数约为332000人,创历史新高,其中数据332000用科学记数法表示为( )
| A. | 0.332×106 | B. | 3.32×105 | C. | 3.32×104 | D. | 33.2×104 |
9. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )| A. | 大于0 | B. | 等于0 | C. | 小于0 | D. | 不能确定 |
14.把x2+x+m因式分解得(x-1)(x+2),则m的值为( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |