题目内容
6.计算:(1)$\sqrt{12x}-\sqrt{\frac{1}{2}x}+\sqrt{\frac{1}{27}x}-\sqrt{50x}$
(2)$({\frac{3}{2}\sqrt{3}-\sqrt{12}})÷\frac{1}{2}\sqrt{3}$;
(3)$\frac{1}{2}$$\sqrt{10}$•(3$\sqrt{15}$-5$\sqrt{6}$)
(4)$({2\sqrt{5}-\sqrt{3}}){\;}^2$.
分析 (1)先把各二次根式化为最简二次根式,然后合并即可;
(2)根据二次根式的除法法则运算;
(3)根据二次根式的乘法法则运算;
(4)利用完全平方公式计算.
解答 解:(1)原式=2$\sqrt{3x}$-$\frac{\sqrt{2x}}{2}$+$\frac{\sqrt{3x}}{9}$-5$\sqrt{2x}$
=$\frac{19\sqrt{3x}}{9}$-$\frac{11\sqrt{2x}}{2}$;
(2)原式=$\frac{3}{2}$•2-2$\sqrt{4}$
=3-4
=-1;
(3)原式=$\frac{3}{2}$$\sqrt{10×15}$-$\frac{5}{2}$$\sqrt{10×6}$
=$\frac{15\sqrt{6}}{2}$-5$\sqrt{15}$;
(4)原式=20-4$\sqrt{15}$+3
=23-4$\sqrt{15}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
9. 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
 二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )
二次函数y=ax2+bx+c(a≠0)和正比例函数y=$\frac{2}{3}$x的图象如图所示,则方程ax2+(b-$\frac{2}{3}$)x+c=0(a≠0)的两根之和( )| A. | 大于0 | B. | 等于0 | C. | 小于0 | D. | 不能确定 |
17.为了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽去了1000名学生的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( )
| A. | 1000名九年级学生是总体的一个样本 | |
| B. | 样本容量是1000 | |
| C. | 2013年昆明市九年级学生是总体 | |
| D. | 每一名九年级学生是个体 |
14.把x2+x+m因式分解得(x-1)(x+2),则m的值为( )
| A. | 2 | B. | 3 | C. | -2 | D. | -3 |
15.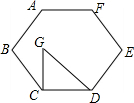 如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )
如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )
 如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )
如图,正六边形ABCDEF的边CD与等腰三角形GCD的直角边CD重合,∠GCD=90°,点G在正六边形的内部,则∠EDG的度数为( )| A. | 90° | B. | 85° | C. | 65° | D. | 75° |
 如图,AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,求EF的长.
如图,AB是⊙O的直径,弦CD⊥AB,垂足是G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,求EF的长.