题目内容
9.正六边形的边长为6,则它的半径为6,边心距为3$\sqrt{3}$,面积为54$\sqrt{3}$.分析 先根据题意画出图形,再根据正六边形的性质求出∠BOC的度数,判断出△BOC为等边三角形即可求出答案.
解答 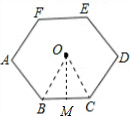 解:如图所示,连接OB、OC;
解:如图所示,连接OB、OC;
∵此六边形是正六边形,
∴∠BOC=360°÷6=60°,
∵OB=OC,
∴△BOC是等边三角形,
∴OB=OC=BC=6.
作OM⊥BC于M点,
∴∠BOM=$\frac{1}{2}$∠BOC=30°,
∴OM=OB•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
∴正六边形的面积=6S△BOC=6×$\frac{1}{2}$×6×3$\sqrt{3}$=54$\sqrt{3}$.
故答案为:6,3$\sqrt{3}$,54$\sqrt{3}$.
点评 本题考查了正多边形与圆的知识,解答此题的关键是根据题意画出图形,作出辅助线;由正六边形的性质判断出△BOC的形状是解答此题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
19.使分式$\frac{2}{1-3x}$的值为正值的条件是( )
| A. | x<$\frac{1}{3}$ | B. | x>$\frac{1}{3}$ | C. | x<0 | D. | x>0 |
20.下列命题中,错误的是( )
| A. | 平分弦的直径垂直于弦 | |
| B. | 直径是圆中最长的弦 | |
| C. | 垂直于弦的直径平分弦 | |
| D. | 弦的垂直平分线平分弦所对的两条弧 |
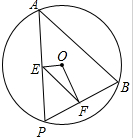 如图,点A,B是⊙O上两点,点P是⊙O0上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.
如图,点A,B是⊙O上两点,点P是⊙O0上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足. 如图,∠B=∠C=90°.点M是BC的中点,DM平分∠ADC.求证:∠BAM=∠DAM.
如图,∠B=∠C=90°.点M是BC的中点,DM平分∠ADC.求证:∠BAM=∠DAM.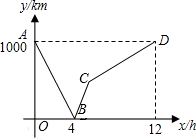 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是③.
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是③.