题目内容
14.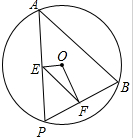 如图,点A,B是⊙O上两点,点P是⊙O0上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.
如图,点A,B是⊙O上两点,点P是⊙O0上的动点(P与A,B不重合),连接AP,BP,过点O分别作OE⊥AP,OF⊥BP,点E、F分别是垂足.(1)求证:∠OEF+∠OFE=∠P;
(2)EF=5,点O到AB的距离为2,求⊙O的半径的长.
分析 (1)由三角形内角和定理和四边形内角和定理即可得出结论;
(2)由垂径定理可以得到E、F分别是AP、BP的中点,然后利用中位线定理求出AB,过O作OC⊥AB于C,连接OB,利用垂径定理和勾股定理即可求解.
解答 (1)证明:∵OE⊥AP,OF⊥BP,
∴∠OEP=∠OFP=90°,
∴∠P+∠EOF=360°-90°-90°=180°,
∵∠OEF+∠OFE+∠EOF=180°,
∴∠OEF+∠OFE=∠P;
(2)解:∵OE⊥AP,OF⊥BP,点E、F分别是垂足,
∴AE=EP,PF=BF,
∴EF是△ABP的中位线,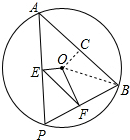
∴EF=$\frac{1}{2}$AB,
∴AB=2EF=10;
过O作OC⊥AB于C,连接OB,如图所示:
则AC=BC=$\frac{1}{2}$AB=5,∠OCB=90°,
∴BC=5,
∴OB=$\sqrt{{2}^{2}+{5}^{2}}$=$\sqrt{29}$,
∴⊙O的半径为$\sqrt{29}$.
点评 此题考查了垂径定理、三角形中位线定理、勾股定理、三角形内角和定理、四边形内角和定理;解题时根据垂径定理证明中位线,然后利用勾股定理计算即可解决问题(2).

练习册系列答案
相关题目
4. 如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )
如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )
 如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )
如图所示,在建筑物AB的底部a米远的C处,测得建筑物的顶端A点的仰角为α,则建筑物AB的高可表示为( )| A. | AB=asinα | B. | AB=$\frac{a}{cosα}$ | C. | AB=$\frac{a}{tanα}$ | D. | AB=a•tanα |