题目内容
1．
如图，∠B=∠C=90°．点M是BC的中点，DM平分∠ADC．求证：∠BAM=∠DAM．
分析 过点M作ME⊥AD，垂足为E，先求出ME=MC，再求出ME=MB，从而证明AM平分∠DAB；
解答 证明：过点M作ME⊥AD，垂足为E，
∵DM平分∠ADC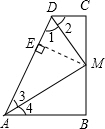
，
∴∠1=∠2，
∵MC⊥CD，ME⊥AD，
∴ME=MC（角平分线上的点到角两边的距离相等），
又∵MC=MB，
∴ME=MB，
∵MB⊥AB，ME⊥AD，
∴AM平分∠DAB，
∴∠BAM=∠DAM．
点评 本题考查的是角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．
练习册系列答案
相关题目
11．下列函数中，y是x的反比例函数的是（ ）
| A． | y=$\frac{x}{7}$ | B． | y=$\frac{1}{2x}$ | C． | y=$\frac{1}{7-x}$ | D． | y=2x |
12．整理一批图书，由一个人做要40小时完成，现在计划由一部分人先做4小时，再增加2人和他们一起做8小时，完成这项工作，假设这些人的工作效率相同，具体先安排多少人工作？
（1）按要求填写下表：
解：设具体应先安排x人工作，，依题意得：
（2）从题目中，你能发现有哪些相等关系吗？（请列出方程）$\frac{4x}{40}$+$\frac{8（x+2）}{40}$=1．
（1）按要求填写下表：
解：设具体应先安排x人工作，，依题意得：
| 类别 相关的量 | 第一时段 | 第二时段 | 备注 |
| 工作效率 | $\frac{1}{40}$ | $\frac{1}{40}$ | $\frac{1}{4}$ |
| 工作时间 | 4 | 8 | 12 |
| 工作人数 | 2 | 4 | 4 |
| 工作总量 | $\frac{1}{5}$ | $\frac{4}{5}$ | 1 |
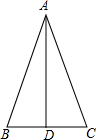如图，在△ABC中，AD平分∠BAC，AD平分BC．求证：△ABC是等腰三角形．
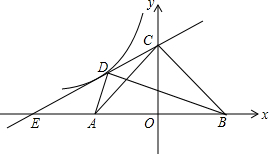如图，直线y=$\frac{1}{2}$x+2交坐标轴于E，C两点，A（-2，0），B（2，0），D为直线上一点，且AD⊥BD，反比例函数y=$\frac{k}{x}$（x＜0）经过D点．
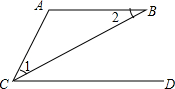在一次数学兴趣小组活动中，老师借助如图，写下了三个式子：