题目内容
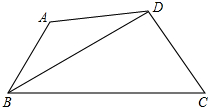 如图,AB<BC,BD平分∠ABC,AD=DC,求证:∠BAD+∠BCD=180°.
如图,AB<BC,BD平分∠ABC,AD=DC,求证:∠BAD+∠BCD=180°.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:过点D作DE⊥AB交BA的延长线于E,DF⊥BC于F,易证△AED≌△CFD,即可求得∠DAE=∠BCD,即可解题.
解答:证明:过点D作DE⊥AB交BA的延长线于E,DF⊥BC于F,
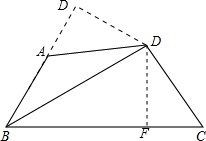
∵BD平分∠ABC,DE⊥AB,DF⊥BC
∴DE=DF,∠AED=∠CFD=90°,
∵在△AED和△CFD中,
,
∴△AED≌△CFD,(HL)
∴∠DAE=∠BCD,
∵∠BAD+∠DAE=180°,
∴∠BAD+∠BCD=180°.

∵BD平分∠ABC,DE⊥AB,DF⊥BC
∴DE=DF,∠AED=∠CFD=90°,
∵在△AED和△CFD中,
|
∴△AED≌△CFD,(HL)
∴∠DAE=∠BCD,
∵∠BAD+∠DAE=180°,
∴∠BAD+∠BCD=180°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△AED≌△CFD是解题的关键.

练习册系列答案
相关题目
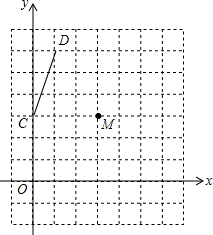 在平面直角坐标系中,已知点C(0,3)、D(1,6),将线段绕点M(3,3)旋转180°后,得到线段AB,则线段AB所在直线的函数解析式是 )
在平面直角坐标系中,已知点C(0,3)、D(1,6),将线段绕点M(3,3)旋转180°后,得到线段AB,则线段AB所在直线的函数解析式是 )| A、y=3x+15 |
| B、y=3x-15 |
| C、y=15x-3 |
| D、y=-15x+3 |
 如图:△ABC分别以AC、BC为边向外作等边△ACD,等边△BCE.连接BD、AE交于点F.试说明:
如图:△ABC分别以AC、BC为边向外作等边△ACD,等边△BCE.连接BD、AE交于点F.试说明: 已知:如图△ABC中,∠A=60°,BD、CE分别是∠ABC和∠ACB的平分线,相交于点F.求证:
已知:如图△ABC中,∠A=60°,BD、CE分别是∠ABC和∠ACB的平分线,相交于点F.求证: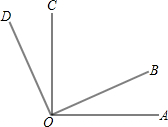 如图,已知∠AOC、∠BOD都是直角,∠AOC+∠AOD=211°,求∠AOB与∠BOC的度数.
如图,已知∠AOC、∠BOD都是直角,∠AOC+∠AOD=211°,求∠AOB与∠BOC的度数.