题目内容
 已知:如图△ABC中,∠A=60°,BD、CE分别是∠ABC和∠ACB的平分线,相交于点F.求证:
已知:如图△ABC中,∠A=60°,BD、CE分别是∠ABC和∠ACB的平分线,相交于点F.求证:(1)∠BFE=60°;
(2)FE=FD.
考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:(1)证明∠EBF=∠CBF=α,∠DCF=∠BCF=β,求出α+β=60°,证明∠BFE=α+β=60°问题即可解决.
(2)证明∠A+∠EFD=180°,得到A、E、F、D四点共圆;证明∠EAF=∠DAF,故FE=FD.
(2)证明∠A+∠EFD=180°,得到A、E、F、D四点共圆;证明∠EAF=∠DAF,故FE=FD.
解答: 证明:(1)∵BD、CE分别是∠ABC和∠ACB的平分线,
证明:(1)∵BD、CE分别是∠ABC和∠ACB的平分线,
∴∠EBF=∠CBF=α,∠DCF=∠BCF=β;
又∵∠A=60°,
∴2α+2β=180°-60°=120°,
∴α+β=60°,
∴∠BFE=α+β=60°.
(2)如图,连接AF;
∵∠BFE=60°,
∴∠EFD=120°,
∴∠A+∠EFD=180°,
∴A、E、F、D四点共圆,设为⊙O;
由题意知在⊙O中,∠EAF=∠DAF,
∴FE=FD(相等的圆周角所对的弦相等).
 证明:(1)∵BD、CE分别是∠ABC和∠ACB的平分线,
证明:(1)∵BD、CE分别是∠ABC和∠ACB的平分线,∴∠EBF=∠CBF=α,∠DCF=∠BCF=β;
又∵∠A=60°,
∴2α+2β=180°-60°=120°,
∴α+β=60°,
∴∠BFE=α+β=60°.
(2)如图,连接AF;
∵∠BFE=60°,
∴∠EFD=120°,
∴∠A+∠EFD=180°,
∴A、E、F、D四点共圆,设为⊙O;
由题意知在⊙O中,∠EAF=∠DAF,
∴FE=FD(相等的圆周角所对的弦相等).
点评:该题主要考查了三角形角平分线的性质、三角形外角的性质、四点共圆的判定及其应用等几何知识点;对综合的分析问题解决问题的能力提出了较高的要求.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
已知二次函数y=a(x+m)2-m(a≠0),无论m为何值,图象的顶点必在( )
| A、直线y=-x上 | B、x轴上 |
| C、y轴上 | D、直线y=x上 |
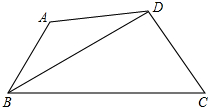 如图,AB<BC,BD平分∠ABC,AD=DC,求证:∠BAD+∠BCD=180°.
如图,AB<BC,BD平分∠ABC,AD=DC,求证:∠BAD+∠BCD=180°. 如图,已知线段AB,在AB的延长线上取一点C,使BC=AB,在AB的反向延长线上取一点D,使DA=
如图,已知线段AB,在AB的延长线上取一点C,使BC=AB,在AB的反向延长线上取一点D,使DA=