题目内容
分解因式：
（1）a2+2a+1；
（2）x2+36+12x；
（3）ax2-4ax+4a；
（4）xy3-2x2y2+x3y．
（1）a2+2a+1；
（2）x2+36+12x；
（3）ax2-4ax+4a；
（4）xy3-2x2y2+x3y．
考点：提公因式法与公式法的综合运用
专题：计算题
分析：（1）原式利用完全平方公式分解即可；
（2）原式利用完全平方公式分解即可；
（3）原式提取a后，利用完全平方公式分解即可；
（4）原式提取公因式后，利用完全平方公式分解即可．
（2）原式利用完全平方公式分解即可；
（3）原式提取a后，利用完全平方公式分解即可；
（4）原式提取公因式后，利用完全平方公式分解即可．
解答：解：（1）原式=（a+1）2；
（2）原式=（x+6）2；
（3）原式=a（x-2）2；
（4）原式=xy（y2-2xy+x2）=xy（y-x）2．
（2）原式=（x+6）2；
（3）原式=a（x-2）2；
（4）原式=xy（y2-2xy+x2）=xy（y-x）2．
点评：此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在式子
、
、
、
+
中，分式的个数有（ ）
| 1 |
| a |
| 3a2b3c |
| 4 |
| 5 |
| 6+x |
| x |
| 7 |
| y |
| 8 |
| A、2个 | B、3个 | C、4个 | D、5个 |
已知二次函数y=a（x+m）2-m（a≠0），无论m为何值，图象的顶点必在（ ）
| A、直线y=-x上 | B、x轴上 |
| C、y轴上 | D、直线y=x上 |
在直角坐标系内，已知A、B两点的坐标分别为A（0，1）、B（3，2），M为x轴上一点，且MA+MB最小，则M的坐标是（ ）
| A、（0，0） |
| B、（1，0） |
| C、（2，0） |
| D、（3，0） |
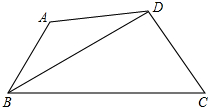如图，AB＜BC，BD平分∠ABC，AD=DC，求证：∠BAD+∠BCD=180°．