题目内容
 如图:△ABC分别以AC、BC为边向外作等边△ACD,等边△BCE.连接BD、AE交于点F.试说明:
如图:△ABC分别以AC、BC为边向外作等边△ACD,等边△BCE.连接BD、AE交于点F.试说明:(1)AE=BD;
(2)∠AFD=60°.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)易证△ACE≌△DCB,根据全等三角形对应边相等的性质即可解题;
(2)根据△ACE≌△DCB可得∠CDB=∠CAE,即可求得∠AFD=60°,即可解题.
(2)根据△ACE≌△DCB可得∠CDB=∠CAE,即可求得∠AFD=60°,即可解题.
解答:解:(1)∵∠ACD=∠BCE=60°,
∴∠BCD=∠ACE,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)∵△ACE≌△DCB,
∴∠CDB=∠CAE,
∵∠FDA+∠FAD=(∠CDA-∠CDB)+(∠CAD+∠CAE),
∴∠FDA+∠FAD=∠CDA+∠CAD=120°,
∴∠AFD=180°-120°=60°.
∴∠BCD=∠ACE,
在△ACE和△DCB中,
|
∴△ACE≌△DCB(SAS),
∴AE=BD;
(2)∵△ACE≌△DCB,
∴∠CDB=∠CAE,
∵∠FDA+∠FAD=(∠CDA-∠CDB)+(∠CAD+∠CAE),
∴∠FDA+∠FAD=∠CDA+∠CAD=120°,
∴∠AFD=180°-120°=60°.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边、对应角相等的性质,本题中求证△ACE≌△DCB是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在直角坐标系内,已知A、B两点的坐标分别为A(0,1)、B(3,2),M为x轴上一点,且MA+MB最小,则M的坐标是( )
| A、(0,0) |
| B、(1,0) |
| C、(2,0) |
| D、(3,0) |
 已知,如图,AB=CD,AE=CF,BE=DF,求证:AF∥CE.
已知,如图,AB=CD,AE=CF,BE=DF,求证:AF∥CE.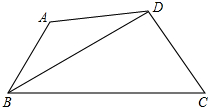 如图,AB<BC,BD平分∠ABC,AD=DC,求证:∠BAD+∠BCD=180°.
如图,AB<BC,BD平分∠ABC,AD=DC,求证:∠BAD+∠BCD=180°.