题目内容
在△ABC中,若3∠A=5∠B,3∠C=2∠B,试判断△ABC的形状.
考点:三角形内角和定理
专题:
分析:设∠B=x,表示出∠A、∠C,然后利用三角形的内角和等于180°列方程求解得到x,再求出最大的内角的度数,再判断三角形的形状即可.
解答:解:设∠B=x,则∠A=
x,∠C=
x,
∵∠A+∠B+∠C=180°,
∴
x+x+
x=180°,
解得x=54°,
所以,最大的内角∠A=54°×
=90°,
所以,△ABC是直角三角形.
| 5 |
| 3 |
| 2 |
| 3 |
∵∠A+∠B+∠C=180°,
∴
| 5 |
| 3 |
| 2 |
| 3 |
解得x=54°,
所以,最大的内角∠A=54°×
| 5 |
| 3 |
所以,△ABC是直角三角形.
点评:本题考查了三角形的内角和定理,把∠A、∠C用∠B表示,然后列出方程是解题的关键.

练习册系列答案
相关题目
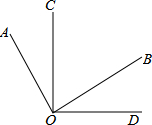 如图,∠AOB,∠COD都是直角,下列结论:①∠AOC=∠BOD;②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线.其中正确的个数有( )
如图,∠AOB,∠COD都是直角,下列结论:①∠AOC=∠BOD;②∠AOC+∠BOD=90°;③若OC平分∠AOB,则OB平分∠COD;④∠AOD的平分线与∠COB的平分线是同一条射线.其中正确的个数有( ) 如图,l是线段AB的对称轴,l′是线段BC的对称轴,l和l′相交于点O.OA与OC相等吗?为什么?
如图,l是线段AB的对称轴,l′是线段BC的对称轴,l和l′相交于点O.OA与OC相等吗?为什么?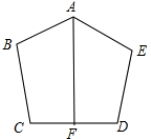 如图,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD于F.
如图,已知AB=AE,BC=ED,∠B=∠E,AF⊥CD于F.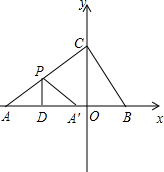 Rt△ABC中,∠ACB=90°,∠CAB=30°,点A、B、C在坐标轴上,点C的坐标为(0,2),点D在射线AB上运动,过点D作PD⊥AB,交直线AC于点P,作过点A关于PD的对称点A′,连接PA′,点D的运动速度为每秒
Rt△ABC中,∠ACB=90°,∠CAB=30°,点A、B、C在坐标轴上,点C的坐标为(0,2),点D在射线AB上运动,过点D作PD⊥AB,交直线AC于点P,作过点A关于PD的对称点A′,连接PA′,点D的运动速度为每秒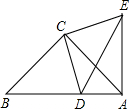 如图,△ABC与△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,DB=4,AB=7,求DE的长.
如图,△ABC与△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,DB=4,AB=7,求DE的长.