题目内容
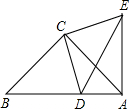 如图,△ABC与△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,DB=4,AB=7,求DE的长.
如图,△ABC与△CDE都是等腰直角三角形,∠ACB=∠DCE=90°,DB=4,AB=7,求DE的长.考点:全等三角形的判定与性质,勾股定理,等腰直角三角形
专题:
分析:根据条件证明△BCD≌△ACE,求得AE和AD,再证明△ADE是直角三角形,在△ADE中由勾股定理求出DE即可.
解答:解:∵∠ACB=∠DCE=90°
∴∠BCD+∠DCA=∠DCA+∠ACE=90°
即∠BCD=∠ACE
∵△ABC与△CDE都为等腰直角三角形
∴BC=AC CD=CE
∠CBD(∠CBA)=∠CAB=45°
在△BCD和△ACE中
∴△BCD≌△ACE(SAS)
∴∠CAE=∠CBD=45°
BD=AE=4
∴∠CAB+∠CAE=45°+45°=90°
∴△ADE是直角三角形
AD=AB-BD=7-4=3
∴DE=
=
=5.
∴∠BCD+∠DCA=∠DCA+∠ACE=90°
即∠BCD=∠ACE
∵△ABC与△CDE都为等腰直角三角形
∴BC=AC CD=CE
∠CBD(∠CBA)=∠CAB=45°
在△BCD和△ACE中
|
∴△BCD≌△ACE(SAS)
∴∠CAE=∠CBD=45°
BD=AE=4
∴∠CAB+∠CAE=45°+45°=90°
∴△ADE是直角三角形
AD=AB-BD=7-4=3
∴DE=
| AE2+AD2 |
| 42+32 |
点评:本题主要考查三角形全等的判定和性质及等腰三角形的性质,解题的关键是证明△ADE是直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知:如图所示,D在△ABC上,且DE∥BC交AC于E,F在AD上,且AD2=AF•AB,求证:△AEF∽△ACD.
已知:如图所示,D在△ABC上,且DE∥BC交AC于E,F在AD上,且AD2=AF•AB,求证:△AEF∽△ACD.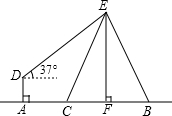 如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)
如图,在电线杆上的E处引拉线EC和EB固定电线杆,在离电线杆6米的A处安置测角仪(点A,C,F在一直线上),在D处测得电线杆上E处的仰角为37°,已知测角仪的高AD为1.5米,AC为3米,求拉线EC的长.(精确到0.1米)