题目内容
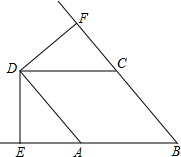 如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形.
如图,D是∠EBF内部的点,DE⊥BE,DF⊥BF,DE=DF,∠FDA=∠EDC,DC=BC,求证:四边形DABC是菱形.考点:菱形的判定
专题:证明题
分析:连接BD,首先利用HL证得Rt△BDF≌Rt△BDE,从而得到∠CDB=∠CBD=∠ABD=∠ADB,进一步得到AB=BC=CD=DA,利用四边相等的四边形是菱形判定结论即可.
解答: 证明:连接BD,
证明:连接BD,
∵DE⊥BE,DF⊥BF,
∴∠DFC=∠DEA=90°,
在Rt△BDF和Rt△BDE中,
,
∴Rt△BDF≌Rt△BDE(HL),
∴∠BDF=∠BDE,
∵∠FDC=∠EDA,
∴∠CDB=∠ADB,
∵DE⊥BE,DF⊥BF,DE=DF,
∴∠FBD=∠EBD,
∵DC=BC,
∴∠CDB=∠CBD=∠ABD=∠ADB,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形.
 证明:连接BD,
证明:连接BD,∵DE⊥BE,DF⊥BF,
∴∠DFC=∠DEA=90°,
在Rt△BDF和Rt△BDE中,
|
∴Rt△BDF≌Rt△BDE(HL),
∴∠BDF=∠BDE,
∵∠FDC=∠EDA,
∴∠CDB=∠ADB,
∵DE⊥BE,DF⊥BF,DE=DF,
∴∠FBD=∠EBD,
∵DC=BC,
∴∠CDB=∠CBD=∠ABD=∠ADB,
∴AB=BC=CD=DA,
∴四边形ABCD是菱形.
点评:本题考查了菱形的判定,解题的关键是了解菱形的判定定理并选择一种最合适的证明方法,难度不大.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
点P(2,-1)在反比例函数y=
(k≠0)的图象上,则k的值是( )
| -k |
| x |
| A、2 | ||
B、
| ||
| C、-2 | ||
D、-
|
 如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )| A、35° | B、45° |
| C、55° | D、65° |
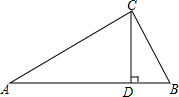 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=2,BC=1,则sin∠ACD=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢?
如图,在一张半透明的纸上画一条直线l,在l外任取一点Q,折出过点P且与l垂直的直线,这样的直线能折出几条?为什么?过点Q呢? 如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数.
如图,已知:圆的两弦AB、CD相交于点P,AD、CB的延长线相交于圆外一点Q,∠AQC=36°,∠APC=80°.求∠ADC和∠BCD的度数.
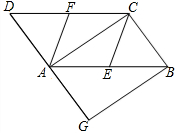 如图,在?ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.
如图,在?ABCD中,E、F分别为边AB、CD的中点,AC是对角线,过点B作BG∥AC交DA的延长线于点G.