题目内容
12.一次函数y=3-x与y=3x-5的图象的交点为(2,1),则方程组$\left\{\begin{array}{l}{x+y=3}\\{3x-y=5}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.分析 根据两函数交点即为两函数组成的方程组的解,从而求出答案.
解答 解:∵一次函数y=3-x与y=3x-5的图象的交点为(2,1),
∴方程组$\left\{\begin{array}{l}{x+y=3}\\{3x-y=5}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
故答案为$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程组交点问题,可直接根据交点写出.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.计算(-$\frac{1}{7}$)÷(-7)的结果为( )
| A. | 1 | B. | -1 | C. | $\frac{1}{49}$ | D. | -$\frac{1}{49}$ |
2.已知a,b,c满足$\frac{a}{2}$=$\frac{b-c}{3}$=$\frac{a+c}{5}$,则$\frac{a+c}{2a+b}$的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | 1 | D. | 2 |
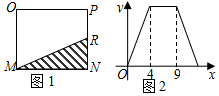 如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,y的值为10.
如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,y的值为10.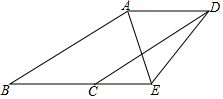 已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.
已知如图,∠ABC=∠ADC,AB∥CD,AE平分∠BAD,当∠ADC:∠CDE=3:2,且∠AED=60°时,求∠BED的度数为$\frac{960}{7}$度.