题目内容
10．等腰三角形的周长为2+$\sqrt{3}$，腰长为1，则底角等于（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 75° |
分析 作底边上的高，根据底和腰的关系可求得底角的余弦值，可求得底角．
解答 
解：∵△ABC的周长为2+$\sqrt{3}$，腰长为1，
AB=AC=1，BC=$\sqrt{3}$，
过A作AD⊥BC于点D，则BD=$\frac{\sqrt{3}}{2}$，
在Rt△ABD中，cos∠B=$\frac{BD}{AB}$=$\frac{\sqrt{3}}{2}$，
∴∠B=30°，
即等腰三角形的底角为30°．
故选：A．
点评 本题主要考查等腰三角形的性质，掌握特殊角的三角函数值是解题的关键．
练习册系列答案
相关题目
3．
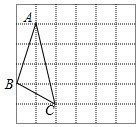如图，在如图的网格中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点．已知A（-2，2）、C（-1，-2），将△ABC绕着点C顺时针旋转90°，则点A对应点的坐标为（ ）
如图，在如图的网格中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点．已知A（-2，2）、C（-1，-2），将△ABC绕着点C顺时针旋转90°，则点A对应点的坐标为（ ）| A． | （2，-2） | B． | （-5，-3） | C． | （2，2） | D． | （3，-1） |
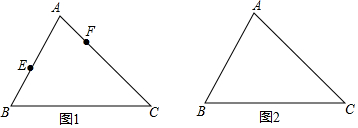
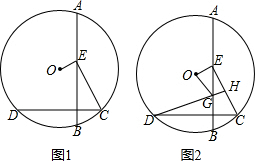
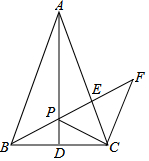在等腰三角形ABC中，AB=AC，AD⊥BC于点D，CF∥AB，P为AD上一点，连结并延长BP交AC于点E，交CF于点F，求证：