题目内容
20.解方程(1)(x-4)2=2x-8
(2)y2-6y-7=0
(3)(2x+1)(x-3)=2.
分析 (1)因式分解法求解可得;
(2)因式分解法求解可得;
(3)公式法求解可得
解答 解:(1)原方程可化为(x-4)2-2(x-4)=0,
∴(x-4)(x-6)=0,
∴x-4=0或x-6=0,
解得:x1=4,x2=6;
(2)(y+1)(y-7)=0,
∴y+1=0或y-7=0,
解得:y1=-1,y2=7;
(3)原方程可化为:2x2-5x-5=0,
∵a=2,b=-5,c=-5,
∴△=25+40=65>0,
∴x=$\frac{5±\sqrt{65}}{4}$,
∴x1=$\frac{5+\sqrt{65}}{4}$,x2=$\frac{5-\sqrt{65}}{4}$.
点评 本题主要考查解一元二次方程的能力,根据不同的方程选择合适的方法是解题的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
10.等腰三角形的周长为2+$\sqrt{3}$,腰长为1,则底角等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
8.若二次根式$\sqrt{x-4}$有意义,则x的取值范围是( )
| A. | x>4 | B. | x≥4 | C. | x≤4 | D. | x≠4 |
15.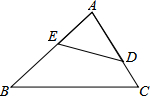 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )
 如图,下列条件不能判定△ABC与△ADE相似的是( )
如图,下列条件不能判定△ABC与△ADE相似的是( )| A. | $\frac{AE}{AC}=\frac{AD}{AB}$ | B. | ∠B=∠ADE | C. | ∠C=∠AED | D. | $\frac{AE}{AC}=\frac{DE}{BC}$ |
5.下列式子中,正确的是( )
| A. | -(-8)>|-11| | B. | $-\frac{1}{5}$<$-\frac{1}{3}$ | C. | |-8|<0 | D. | -5<-(-3) |
10.某市区某天的最高气温是8℃,最低气温是零下4℃,则该地这一天的温差是( )
| A. | -10℃ | B. | -8℃ | C. | 8℃ | D. | 12℃ |
 如图3所示,数轴的一部分被墨水污染,被污染的部分内含有的整数为-2,-1,0,1.
如图3所示,数轴的一部分被墨水污染,被污染的部分内含有的整数为-2,-1,0,1.