题目内容
15.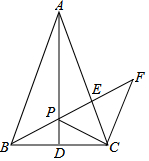 在等腰三角形ABC中,AB=AC,AD⊥BC于点D,CF∥AB,P为AD上一点,连结并延长BP交AC于点E,交CF于点F,求证:
在等腰三角形ABC中,AB=AC,AD⊥BC于点D,CF∥AB,P为AD上一点,连结并延长BP交AC于点E,交CF于点F,求证:(1)△ABP≌△ACP;
(2)BP2=PE•PF.
分析 (1)利用等腰三角形的性质得出结论,即可判断出结论;
(2)要证线段乘积式相等,常常先证比例式成立,要证比例式,须有三角形相似,要证三角形相似,须根据已知与图形找条件就可.
解答 解:(1)证明:
∵AB=AC,AD⊥BC,
∴AD是△ABC的对称轴.
∴PC=PB,∠PCE=∠ABP.
在△ABP和△ACP中,$\left\{\begin{array}{l}{AB=AC}\\{AP=AP}\\{BP=CP}\end{array}\right.$,
∴△ABP和≌△ACP,
(2)∵CF∥AB,
∴∠PFC=∠ABP(两直线平行,内错角相等),
∴∠PCE=∠PFC.
又∵∠CPE=∠EPC,
∴△EPC∽△CPF.
∴(相似三角形的对应边成比例).
∴PC2=PE•PF.
∵PC=BP
∴BP2=PE•PF.
点评 此题是相似三角形的判定和性质,主要考查了全等三角形的判定和性质,证明线段乘积式相等,常常先证比例式成立这是十分重要的方法之一,本题主要考查的是相似三角形性质的应用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
8.一个两位数的个位数字是a,十位数字是b(b≠0),用代数式表示这个两位数为( )
| A. | 10b+a | B. | 10a+b | C. | b+a | D. | 100a+10b |
10.等腰三角形的周长为2+$\sqrt{3}$,腰长为1,则底角等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
4. 把如图的纸片按虚线折叠成纸盒,可以得到( )
把如图的纸片按虚线折叠成纸盒,可以得到( )
 把如图的纸片按虚线折叠成纸盒,可以得到( )
把如图的纸片按虚线折叠成纸盒,可以得到( )| A. |  | B. |  | C. |  | D. |  |
5.下列式子中,正确的是( )
| A. | -(-8)>|-11| | B. | $-\frac{1}{5}$<$-\frac{1}{3}$ | C. | |-8|<0 | D. | -5<-(-3) |
 如图,A点的坐标是(0,6),AB=BO,∠ABO=120°,C在x轴上运动,在坐标平面内作点D,使AD=DC,∠ADC=120°,连结OD,则OD的长的最小值为$\sqrt{3}$.
如图,A点的坐标是(0,6),AB=BO,∠ABO=120°,C在x轴上运动,在坐标平面内作点D,使AD=DC,∠ADC=120°,连结OD,则OD的长的最小值为$\sqrt{3}$. 如图,AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
如图,AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论:
如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(-1,0),其部分图象如图所示,下列结论: