题目内容
20.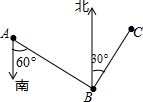 如图,点B在点A的南偏东60°方向,点C在点B的北偏东30°方向,且BC=12km,则点C到直线AB的距离是12km.
如图,点B在点A的南偏东60°方向,点C在点B的北偏东30°方向,且BC=12km,则点C到直线AB的距离是12km.
分析 根据平行线的性质求出∠EBA的度数,得到∠ABC为直角,求出点C到直线AB的距离.
解答 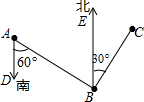 解:∵AD∥BE,
解:∵AD∥BE,
∴∠EBA=∠A=60°,
∴∠ABC=∠ABE+∠CBE=90°,
∴点C到直线AB的距离是BC,即12km,
故答案为:12km.
点评 本题考查的是方位角和点到直线的距离,正确理解方位角和点到直线的距离的概念是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.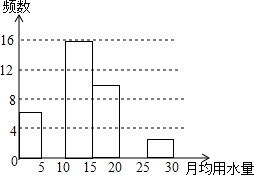 八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
(1)求出a,b的值,并把频数分布直方图补充完整.
(2)求月均用水量不超过15t的家庭数占被调查家庭总数的百分比.
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
 八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:
八年级(2)班同学为了解2015年某小区家庭1月份用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理:| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | a | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | b |
| 25<x≤30 | 2 | 0.04 |
(2)求月均用水量不超过15t的家庭数占被调查家庭总数的百分比.
(3)若该小区有1000户家庭,根据调查数据估计,该小区月均用水量超过20t的家庭大约有多少户?
15.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表,从表中可知,下列说法错误的是( )
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -10 | -4 | 0 | 2 | 2 | … |
| A. | 抛物线的对称轴为x=$\frac{1}{2}$ | |
| B. | 抛物线与x轴的另一个交点为(2,0) | |
| C. | 抛物线与直线y=2的两个交点之间的距离为1 | |
| D. | 在对称轴右侧,y随x增大而增大 |
 如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点 O恰好落在延长线上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.
如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点 O恰好落在延长线上点D处,折痕交OA于点C,整个阴影部分的面积9π-12$\sqrt{3}$.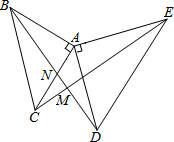 如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,CE与BD相交于点M,BD交AC于点N.求证:BD⊥CE.
如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,CE与BD相交于点M,BD交AC于点N.求证:BD⊥CE.
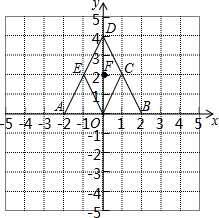 如图,指出坐标平面内各点的坐标:A(-2,0),C(1,2),F(0,2).
如图,指出坐标平面内各点的坐标:A(-2,0),C(1,2),F(0,2).