题目内容
15.抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y的对应值如表,从表中可知,下列说法错误的是( )| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -10 | -4 | 0 | 2 | 2 | … |
| A. | 抛物线的对称轴为x=$\frac{1}{2}$ | |
| B. | 抛物线与x轴的另一个交点为(2,0) | |
| C. | 抛物线与直线y=2的两个交点之间的距离为1 | |
| D. | 在对称轴右侧,y随x增大而增大 |
分析 由表中数据可知当x=0时和x=1时的函数值相等,可求得对称轴,可判断A;由对称性可求得抛物线与x轴的交点坐标,可判断B;由表中所给数据可知当y=2时对应的x的值可判断C;由数据可知抛物线开口向下,可判断D;可得出答案.
解答 解:∵当x=0和x=1时,y=2,
∴抛物线对称轴为x=$\frac{1+0}{2}$=$\frac{1}{2}$,
故A正确;
∵x=-1时,y=0,
∴由对称性可知x=2时,y=0,
∴抛物线与x轴的另一交点坐标为(2,0),
故B正确;
∵当x=0和x=1时,y=2,
∴抛物线与直线y=2的交点为(0,2)和(1,2)
∴两交点之间的距离为1,
故C正确;
由表中所给数据可知当x>$\frac{1}{2}$,y随x的增大而减小,
故D不正确;
故选D.
点评 本题主要考查二次函数的性质,掌握二次函数的对称轴、与x轴的交点及增减性是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.已知O为四边形ABCD对角线的交点,下列条件能使四边形ABCD成为矩形的是( )
| A. | OA=OC,OB=OD | B. | AC=BD | ||
| C. | AC⊥BD | D. | ∠ABC=∠BCD=∠CDA=90° |
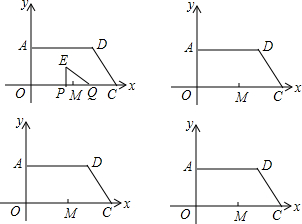
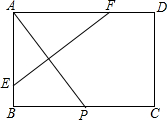 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点.现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E,F.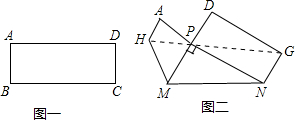 把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,
把图一的长方形纸片ABCD折叠,B、C两点恰好重合落在AD边上的点P处(如图二),已知∠MPN=90°,PM=3,PN=4,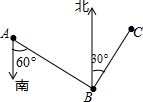 如图,点B在点A的南偏东60°方向,点C在点B的北偏东30°方向,且BC=12km,则点C到直线AB的距离是12km.
如图,点B在点A的南偏东60°方向,点C在点B的北偏东30°方向,且BC=12km,则点C到直线AB的距离是12km. 如图,在?ABCD中,CE平分∠BCD交AD边于点E,且AD=5,CD=3,则AE长为2.
如图,在?ABCD中,CE平分∠BCD交AD边于点E,且AD=5,CD=3,则AE长为2.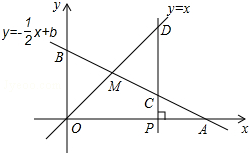 如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.
如图,已知函数y=-$\frac{1}{2}$x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2,在x轴上有一点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=-$\frac{1}{2}$x+b和y=x的图象于点C、D.