题目内容
2.2016年太原市地铁2号线一期工程建设如火如荼.预计2020年底投入运营.从此省城将进入立体大交通新时代.甲、乙两个工程队计划参与其中的一项工程建设,甲队单独施工40天完成该项工程的$\frac{2}{3}$,这时乙队加入,两队还需同时施工8天才能完成该项工程.(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过45天,则乙队至少施工多少天才能完成该项工程?
分析 (1)直接利用队单独施工40天完成该项工程的$\frac{2}{3}$,这时乙队加入,两队还需同时施工8天,进而利用总工作量为1得出等式求出答案;
(2)直接利用甲队参与该项工程施工的时间不超过45天,得出不等式求出答案.
解答 解:(1)设乙队单独施工,需要x天才能完成该项工程,
∵甲队单独施工40天完成该项工程的$\frac{2}{3}$,
∴甲队单独施工60天完成该项工程,
根据题意可得:$\frac{2}{3}$+8×($\frac{1}{60}$+$\frac{1}{x}$)=1,
解得:x=40,
检验得:x=40是原方程的根,
答:乙队单独施工,需要40天才能完成该项工程;
(2)设乙队参与施工y天才能完成该项工程,根据题意可得:$\frac{1}{60}$×45+$\frac{1}{40}$y≥1,
解得:y≥10,
答:乙队至少施工10天才能完成该项工程.
点评 此题主要考查了分式方程的应用以及一元一次不等式的应用,正确得出等量关系是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中心重合,这样得到图②,图③,…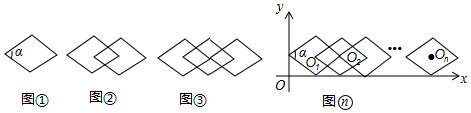
(1)观察图形并完成表格:
猜想:在图n中,菱形的个数为4n-5[用含有n(n≥3)的代数式表示];
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1,1),则x1=$\sqrt{3}$;第2017个基本图形的中心O2017的坐标为(2017$\sqrt{3}$,1).

(1)观察图形并完成表格:
| 图形名称 | 基本图形的个数 | 菱形的个数 |
| 图① | 1 | 1 |
| 图② | 2 | 3 |
| 图③ | 3 | 7 |
| 图④ | 4 | 11 |
| … | … | … |
(2)如图,将图n放在直角坐标系中,设其中第一个基本图形的中心O1的坐标为(x1,1),则x1=$\sqrt{3}$;第2017个基本图形的中心O2017的坐标为(2017$\sqrt{3}$,1).
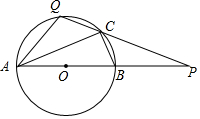 已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上)
已知如图:AB是⊙O的直径,点P在线段AB的延长线上,BP=OB=2,点Q是半圆上一动点(不与A、B重合),连接PQ,交⊙O于点C.下列结论:①∠QAP=∠BCP;②$\frac{CP}{QP}$=$\frac{BP}{AP}$;若点Q为劣弧$\widehat{AC}$的中点,则C是PQ的中点;④若点Q与C重合时,则PQ=2$\sqrt{3}$.其中正确的是①③④0(把所有正确结论的序号都选上) 从一副扑克牌中取出方块3、红心6、黑挑10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字、这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同,则为平局.
从一副扑克牌中取出方块3、红心6、黑挑10共三张牌,洗匀后正面朝下放在桌面上,小明和小丽玩摸牌游戏,游戏规则如下:先由小明随机摸出一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小丽随机摸出一张牌,记下牌面数字、这样记为一次游戏.当两人摸出的牌面数字不同时,牌面数字大的获胜;当两人摸出的牌面数字相同,则为平局.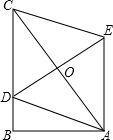 如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,求DE的最小值.
如图,在Rt△ABC中,∠B=90°,AB=4,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,求DE的最小值. 如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.
如图所示.在?ABCD中.E、F分别是边AD、BC上的点,连接AF、BE交于点G:连接CE、DF交于点H,连接GH.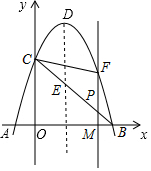 如图,抛物线y=-x2+2x+3与x轴相交于A、B两点,与y轴相交于点C,顶点为D.
如图,抛物线y=-x2+2x+3与x轴相交于A、B两点,与y轴相交于点C,顶点为D.