题目内容
 作出函数y=
作出函数y=| 1 |
| 2 |
(1)与坐标轴的交点坐标;
(2)x取何值时,y>0?x取何值时,y<0?
(3)图象与坐标轴所围成的三角形面积.
考点:一次函数的图象,一次函数的性质
专题:
分析:(1)令x=0时,y=-2,y=0时,x=4,可确定与坐标轴的交点坐标.
(2)根据图示可以直接得到答案.
(3)根据三角形的面积公式进行解答;
(2)根据图示可以直接得到答案.
(3)根据三角形的面积公式进行解答;
解答:解:(1)当x=0时,y=-2,
当y=0时,x=4,即直线y=
x-2与坐标轴的交点坐标为(0,-2),(4,0),过这两点作直线即为y=
x-2的图象,

(2)根据图象知,当x>4时,y>0,当x<4时,y<0,
(3)∵A(0,-2),B(4,0),
∴OA=2,OB=4
∴S△AOB=
OA•OB=
×2×4=4,即图象与坐标轴围成的三角形面积是4;
当y=0时,x=4,即直线y=
| 1 |
| 2 |
| 1 |
| 2 |

(2)根据图象知,当x>4时,y>0,当x<4时,y<0,
(3)∵A(0,-2),B(4,0),
∴OA=2,OB=4
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了直线与坐标轴的交点,一次函数的性质以及一次函数的图象.解题时,要求学生具备一定的读图能力.

练习册系列答案
相关题目
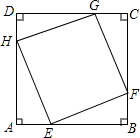 如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4.
如图,点E、F、G、H分别在正方形ABCD的四条边上,并且四边形EFGH也是正方形,AB=4.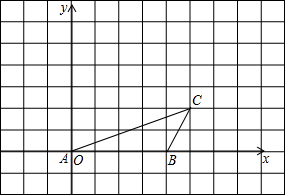 如图,已知点A、B、C的坐标分别为(0,0)、(4,0)、(5,2),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
如图,已知点A、B、C的坐标分别为(0,0)、(4,0)、(5,2),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.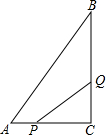 如图所示,在△ABC中,∠C=90°,AC=5cm,BC=7cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
如图所示,在△ABC中,∠C=90°,AC=5cm,BC=7cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.