题目内容
16.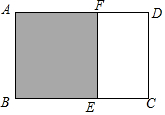 如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为$\frac{{1+\sqrt{5}}}{2}$.
如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为$\frac{{1+\sqrt{5}}}{2}$.
分析 设AD=x,根据正方形的性质得AF=AB=EF=1,则FD=x-1,在根据相似多边形的性质,得到DF:AB=EF:AD,即(x-1):1=1:x,然后解方程,即可得到AD的长.
解答  解:设AD=x,
解:设AD=x,
∵四边形ABEF为正方形,
∴AF=AB=EF=1,
∴FD=x-1,
∵矩形ECDF与矩形ABCD相似,
∴DF:AB=EF:AD,
即(x-1):1=1:x,
整理得x2-x-1=0,
解得x1=$\frac{{1+\sqrt{5}}}{2}$,x2=$\frac{1-\sqrt{5}}{2}$(舍去),
∴AD的长为$\frac{{1+\sqrt{5}}}{2}$.
故答案为:$\frac{{1+\sqrt{5}}}{2}$.
点评 本题考查了相似多边形的性质以及矩形的性质,解题时注意:相似多边形对应边的比叫做相似比;对应角相等;对应边的比相等;相似多边形面积的比等于相似比的平方.

练习册系列答案
相关题目
1.若x1,x2是一元二次方程2x2-x-3=0的两根,则x1+x2的值是( )
| A. | -1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 3 |
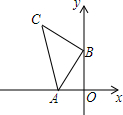 如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,3),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC,则点C的坐标是(-3.5).
如图,在平面直角坐标系中,点A的坐标为(-2,0),点B的坐标为(0,3),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC,则点C的坐标是(-3.5).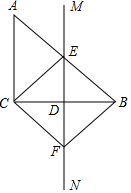 如图,在直角△ABC中,∠ACB=90°,BC的垂直平分线MN交BC于点D,交AB于点E,CF∥AB交MN于点F,连接CE、BF.
如图,在直角△ABC中,∠ACB=90°,BC的垂直平分线MN交BC于点D,交AB于点E,CF∥AB交MN于点F,连接CE、BF. 如图,将三角尺的直角顶点放在直尺的一边上,使∠1=60°,∠2=100°,则∠3=40°.
如图,将三角尺的直角顶点放在直尺的一边上,使∠1=60°,∠2=100°,则∠3=40°.