题目内容
6.($\frac{x+1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$)÷$\frac{x}{x-1}$,然后从不等式组$\left\{\begin{array}{l}-x-2≤3\\ 2x<12\end{array}\right.$的解集中,选取一个你认为符合题意的x的值代入求值.分析 先化简题目中的式子,然后求出不等式组的解集,然后选取一个符号要求的x的值代入化简后的式子即可解答本题,注意x≠0,1.
解答 解:($\frac{x+1}{x-1}$+$\frac{1}{{x}^{2}-2x+1}$)÷$\frac{x}{x-1}$
=$\frac{(x+1)(x-1)+1}{(x-1)^{2}}×\frac{x-1}{x}$
=$\frac{{x}^{2}}{(x-1)^{2}}×\frac{x-1}{x}$
=$\frac{x}{x-1}$,
解不等式组$\left\{\begin{array}{l}-x-2≤3\\ 2x<12\end{array}\right.$,得-5≤x<6,
当x=2时,原式=$\frac{2}{2-1}$=2.
点评 本题考查分式的化简求值,解题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
1.边长为a的正三角形的内切圆的半径为( )
| A. | $\frac{1}{2}$a | B. | $\frac{\sqrt{3}}{2}$a | C. | $\frac{\sqrt{3}}{3}$a | D. | $\frac{\sqrt{3}}{6}$a |
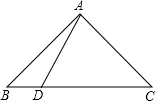 在△ABC中,已知AB=AC=10,BC=16,点D在BC上,且BD=$\frac{7}{2}$,连接AD,求证:AD⊥AC.
在△ABC中,已知AB=AC=10,BC=16,点D在BC上,且BD=$\frac{7}{2}$,连接AD,求证:AD⊥AC.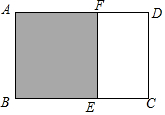 如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为$\frac{{1+\sqrt{5}}}{2}$.
如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为$\frac{{1+\sqrt{5}}}{2}$.