题目内容
6.某班学生去学校食堂打饭,共用了65个碗,吃饭的时候每2个人合用1个饭碗,每3个人合用1个汤碗,每4个人合用1个菜碗.设这个班有学生x人,则所列方程为$\frac{x}{2}+\frac{x}{3}+\frac{x}{4}=65$.分析 设这个班级一共有x人来吃饭,根据题意列出方程解答即可.
解答 解:设这个班有学生x人,可得:$\frac{x}{2}+\frac{x}{3}+\frac{x}{4}=65$,
故答案为:$\frac{x}{2}+\frac{x}{3}+\frac{x}{4}=65$
点评 此题考查一元一次方程的应用,把这个班级来吃饭人数设为x,再用x分别表示出需要饭碗,汤碗以及菜碗个数,再根据它们之间的关系列方程,是解答本题的关键.

练习册系列答案
相关题目
17.如果代数式3x2-4x的值为6,那么6x2-8x-9的值为( )
| A. | 12 | B. | 3 | C. | $\frac{3}{2}$ | D. | -3 |
14.在50包型号为L的衬衫的包裹中混进了型号为M的衬衫,每包20件衬衫,每包中混入的M号衬衫数如表:
根据以上数据,选择正确选项( )
| M号衬衫数 | 0 | 1 | 4 | 5 | 7 | 9 | 10 | 11 |
| 包数 | 7 | 3 | 10 | 15 | 5 | 4 | 3 | 3 |
| A. | M号衬衫一共有47件 | |
| B. | 从中随机取一包,包中L号衬衫数不低于9是随机事件 | |
| C. | 从中随机取一包,包中L号衬衫数不超过4的概率为0.26 | |
| D. | 将50包衬衫混合在一起,从中随机拿出一件衬衫,恰好是M号的概率为0.252 |
11.若|a-1|+(b+3)2=0,则b-a-$\frac{1}{2}$的值为( )
| A. | -5$\frac{1}{2}$ | B. | -4$\frac{1}{2}$ | C. | -3$\frac{1}{2}$ | D. | -1$\frac{1}{2}$ |
18.在△ABC中,∠C=90°,AB=6,cosA=$\frac{1}{3}$,则AC等于( )
| A. | 18 | B. | 2 | C. | $\frac{1}{2}$ | D. | $\frac{1}{18}$ |
5.多项式4x3+7x-2的次数和常数项分别是( )
| A. | 3和2 | B. | 3和-2 | C. | 4和2 | D. | 4和-2 |
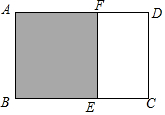 如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为$\frac{{1+\sqrt{5}}}{2}$.
如图,已知矩形纸片ABCD中,AB=1,剪去正方形ABEF,得到的矩形ECDF与矩形ABCD相似,则AD的长为$\frac{{1+\sqrt{5}}}{2}$. 如图,已知△ABC≌△FED,∠A=40°,∠B=106°,则∠EDF=34°.
如图,已知△ABC≌△FED,∠A=40°,∠B=106°,则∠EDF=34°.