题目内容
如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°.AE=DE,AC、BD的交点为O.
(1)求证:△AEC≌△DEB;
(2)若∠ABC=∠DCB=90°,AB=2cm,求图中阴影部分的面积.
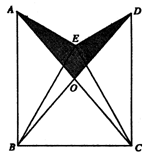
(1)证明略 (2)解:连结EO并延长EO交BC于点F,连结AD.
由(1),知AC=BD.∵∠ABC=∠DCB=90°,
∴∠ABC+∠DCB=180°,AB∥DC,AB=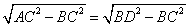 =CD,
=CD,
∴四边形ABCD为平行四边形且矩形.
∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,
∴BF=FC,∠EFB=90°,∴OF=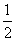 AB=
AB=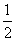 ×2=1,
×2=1,
∵△ BEC是等边三角形,∴∠EBC=60°,
BEC是等边三角形,∴∠EBC=60°,
在 Rt△AEB中,∠AEB=90°,∠ABE=∠ABC-∠EBC=90°-60°=30°,
Rt△AEB中,∠AEB=90°,∠ABE=∠ABC-∠EBC=90°-60°=30°,
∴BE=AB ·cos30°=2×
·cos30°=2×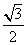 =
=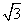 ,
,
在Rt△BFE中,∠BFE=90°,∠EBF=60 °,
°,
∴BF=BE·cos60°=
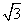 ×
×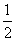 =
=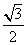 ,EF=BE·sin60°=
,EF=BE·sin60°=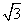 ×
×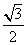 =
=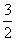 ,
,
∴OE=EF-OF=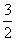 -1=
-1=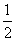 ,
,
∵AE=ED,OE=OE ,AO=DO,∴△AOE≌△DOE,
,AO=DO,∴△AOE≌△DOE,
∴S△AOE=S△DOE,
∴S阴影=2S△AOE =2×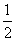 ·EO·BF=2×
·EO·BF=2×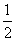 ×
×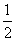 ×
×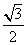 =
=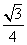 (cm2).
(cm2).

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 )?
)?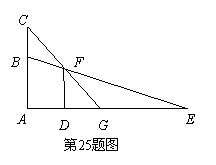

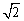 cm,则DC的长为 ( )
cm,则DC的长为 ( ) A.2
A.2 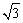 cm B.
cm B. 2
2 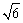 cm C.4 cm D.4
cm C.4 cm D.4


 ( )
( ) B.
B.  C.
C.  D.
D. 
 ;
;